Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online:

Flächen und Oberflächenintegrale

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Sei $ K\subseteq\mathbb{R}^2$ eine kompakte meßbare Menge.

Eine Fläche (im dreidimensionalen Raum) ist eine Funktion $ \Phi:K\to\mathbb{R}^3$ derart, daß es eine offene Obermenge $ O\supseteq K$ gibt und sich $ \Phi$ fortsetzen läßt zu einer stetig differenzierbaren Funktion $ \tilde{\Phi}:O\to\mathbb{R}^3$ .

Der Grund für die Forderung der Existenz der größeren Menge $ O$ und der Fortsetzung $ \tilde{\Phi}$ ist, daß wir auch in Randpunkten von $ K$ die Ableitung von $ \Phi$ betrachten wollen. Kurz gesagt, ist $ \Phi:K\to\mathbb{R}^3$ eine ,,auch auf dem Rand von $ K\;$ `` stetig differenzierbare Funktion.

Die Bildmenge $ \mathcal{T}(\Phi):=\Phi(K)\subseteq\mathbb{R}^3$ heißt der Träger von $ \Phi$ .

Der Normalenvektor $ \mathrm{n}_\Phi$ der Fläche $ \Phi$ ist an jedem Punkt $ (x_1,x_2)^\mathrm{t}\in K$ definiert durch

$\displaystyle \mathrm{n}_{\Phi}(x_1,x_2)\;:=\; \Phi_{x_1}(x_1,x_2)\times\Phi_{x_2}(x_1,x_2)\;. $

Wir erinnnern dabei an die Definition des Kreuzproduktes

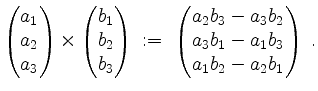
$\displaystyle \begin{pmatrix}a_1\\ a_2\\ a_3\end{pmatrix}\times\begin{pmatrix}b... ...; \begin{pmatrix}a_2b_3-a_3b_2\\ a_3b_1-a_1b_3\\ a_1b_2-a_2b_1\end{pmatrix}\;. $

Das Kreuzprodukt zweier Vektoren ist ein Vektor, der zu beiden Faktoren orthogonal ist, und dessen Länge dem Flächeninhalt des von den beiden Faktoren aufgespannten Parallelogramm entspricht. $ \Phi_{x_1}(x)$ und $ \Phi_{x_2}(x)$ sind zwei Tangentialvektoren in $ \Phi(x)$ an $ \mathcal{T}(\Phi)$ .

Oberflächenintegral eines Vektorfeldes.

Es sei $ f:\mathcal{T}(\Phi)\to\mathbb{R}^3$ ein stetiges Vektorfeld. Dann definieren wir das Oberflächenintegral von $ f$ über $ \Phi$ vermöge

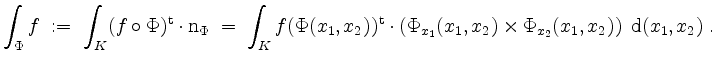
$\displaystyle \int_\Phi f \;:=\; \int_K (f\circ\Phi)^\mathrm{t}\cdot\mathrm{n}_... ...t(\Phi_{x_1}(x_1,x_2) \times\Phi_{x_2}(x_1,x_2)\right)\;\mathrm{d}(x_1,x_2)\;. $

Oberflächenintegral einer skalaren Funktion.

Es sei $ g:\mathcal{T}(\Phi)\to\mathbb{R}$ eine stetige skalare Funktion. Dann definieren wir das Oberflächenintegral von $ g$ über $ \Phi$ vermöge

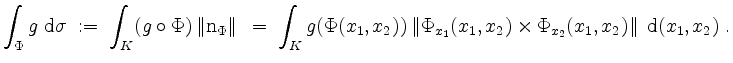
$\displaystyle \displaystyle\int_\Phi g\;\mathrm{d}\sigma \;:=\; \displaystyle\... ...hi_{x_1}(x_1,x_2) \times\Phi_{x_2}(x_1,x_2)\right\Vert\;\mathrm{d}(x_1,x_2)\;. $

Das Integrationselement $ \mathrm{d}\sigma$ steht dabei für die Integration über eine Fläche, englisch ,,surface``.

So ist z.B. der Flächeninhalt der Fläche $ \Phi$ definiert als

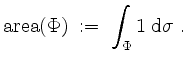
$\displaystyle \mathrm{area}(\Phi) \;:=\; \int_\Phi 1\;\mathrm{d}\sigma\;. $

Das Oberflächenintegral ist in gewissem Sinne nur abhängig vom Träger $ \mathcal{T}(\Phi)$ und von der Orientierung der Fläche. Genauer, ist $ \tilde{K}\subseteq\mathbb{R}^2$ eine weitere kompakte meßbare Menge, $ \tilde{\Phi}:\tilde{K}\to\mathbb{R}^3$ eine stetig differenzierbare Funktion, und ist $ \psi:K\to\tilde{K}$ eine stetig differenzierbare bijektive Abbildung so, daß $ \Phi=\tilde{\Phi}\circ\psi$ und $ \det\psi\,'>0$ überall, so heißen die Flächen $ \Phi$ und $ \tilde{\Phi}$ äquivalent. Es gelten dann

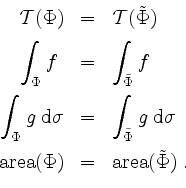
\begin{displaymath} \begin{array}{rcl} \mathcal{T}(\Phi) &=& \mathcal{T}(\tilde{... ...thrm{area}(\Phi) &=& \mathrm{area}(\tilde{\Phi})\;. \end{array}\end{displaymath}

Der Kurvenschwerpunkt und die 2. Guldinsche Regel.

Sei $ \gamma=(\gamma_1,\ldots,\gamma_n)^\mathrm{t}:[a,b]\to\mathbb{R}^n$ ein Weg mit $ \ell(\gamma)>0$ . Dann heißt der Punkt $ (s_1,\ldots,s_n)^\mathrm{t}\in\mathbb{R}^n$ mit den Koordinaten

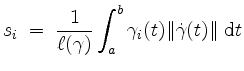
$\displaystyle s_i \;=\; \dfrac{1}{\ell(\gamma)}\int_a^b \gamma_i(t)\Vert\dot{\gamma}(t)\Vert\;\mathrm{d}t $

der Kurvenschwerpunkt von $ \gamma$ .

Sei nun speziell $ \gamma=(\gamma_1,\gamma_2)^\mathrm{t}:[a,b]\to\mathbb{R}_{\geq 0}\times\mathbb{R}$ ein Weg mit Kurvenschwerpunkt $ (s_1,s_2)^\mathrm{t}$ . Sei $ \Phi$ die aus $ \gamma$ entstehende Rotationsfläche bei Drehung um die $ y$ -Achse, d.h. $ \Phi$ ist die Fläche mit der Parametrisierung

$\displaystyle \Phi:[a,b]\times[0,2\pi]\to\mathbb{R}^3\;,\;\; \Phi(t,\varphi) \;... ...amma_1(t)\cos\varphi\;,\;\gamma_2(t)\;,\;\gamma_1(t)\sin\varphi)^\mathrm{t}\;. $

Der 2. Guldinschen Regel zufolge berechnet sich nun den Flächeninhalt von $ \Phi$ zu

$\displaystyle \mathrm{area}(\Phi) \;=\; \ell(\gamma)\cdot 2\pi s_1\;. $

Mit anderen Worten, der Flächeninhalt der Rotationsfläche $ \Phi$ ist gleich der Länge des Weges $ \gamma$ , multipliziert mit der Länge des bei der Rotation zurückgelegten Weges des Kurvenschwerpunktes.
(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Beispiele] [Verweise]
  automatisch erstellt am 11.  8. 2006