Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Funktionen einer Veränderlichen - Rationale Funktionen

Rationale Funktion

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Eine rationale Funktion $ r$ mit Zählergrad $ m$ und Nennergrad $ n$ ist der Quotient zweier Polynome:

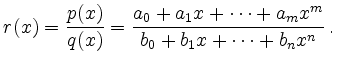
$\displaystyle r(x) = \frac{p(x)}{q(x)} = \frac{a_0+a_1x+\cdots+a_mx^m}{b_0+b_1x+\cdots+b_nx^n} \,. $

Diese Darstellung bezeichnet man als irreduzibel, wenn $ p$ und $ q$ keinen gemeinsamen Linearfaktor besitzen. Die Nullstellen des Nenners sind dann Definitionslücken der rationalen Funktion $ r$ und werden als Polstellen bezeichnet. Ihre Ordnung entspricht der Vielfachheit der Nullstelle.

Die Variable $ x$ und die Koeffizienten $ a_k$, $ b_k$ können reell oder komplex sein. Entsprechend spricht man von einer reellen oder komplexen rationalen Funktion.

Die Funktion

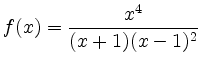
$\displaystyle f(x)=\frac{x^4}{(x+1)(x-1)^2}$

besitzt einen einfachen Pol bei $ x=-1$ und einen doppelten Pol bei $ x=1$.

\includegraphics[width=7.4cm]{xxxx_1+x_1-x_1-x.eps}

Man erkennt aus der Abbildung, dass $ f$ bei einem einfachen Pol das Vorzeichen wechselt und sich das Vorzeichen bei einem doppelten Pol nicht ändert.

(Autoren: App/Höllig )

(Inhalt vorübergehend nicht verfügbar)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017