Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Funktionen einer Veränderlichen - Potenzen und Logarithmen

Logarithmus

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die Logarithmusfunktion ist die Umkehrfunktion der Exponentialfunktion:

$\displaystyle y=e^x \quad \Leftrightarrow\quad x=\ln y .$

\includegraphics[width=7.4cm]{graph_logarithmus}
Sie bildet $ (0,\infty)$ streng monoton wachsend auf $ \mathbb{R}$ ab und erfüllt die Funktionalgleichung

$\displaystyle \ln(xy) = \ln x + \ln y .$

Insbesondere ist $ \ln (1/x)=-\ln x$.
(Inhalt vorübergehend nicht verfügbar)
Der Logarithmus hat die Eigenschaft, dass die Summe der Logarithmen zweier Zahlen gleich dem Logarithmus des Produkts dieser Zahlen ist:

$\displaystyle \log x + \log y = \log (xy). $

Somit kann man zwei Lineale mit logarithmischer Skala aneinanderlegen und erhält als Ergebnis nicht die Summe sondern das Produkt dieser Zahlen (Prinzip des Rechenschiebers).
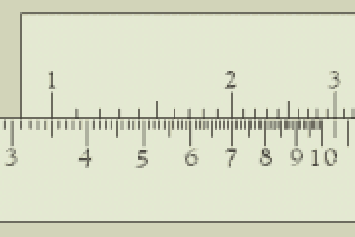
\includegraphics{bsp_rechenschieber_bild}

Aus der Abbildung entnimmt man beispielsweise, dass $ 3.5\cdot 2=7$ . Hierzu wird zunächst die 1 der oberen Skala auf die 3.5 (erster Faktor) der unteren Skala ausgerichtet. Anschließend kann unter der 2 der oberen Skala (zweiter Faktor) das Resultat der Multiplikation auf der unteren Skala abgelesen werden.

(Autoren: Höllig/Kopf/Wipper)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017