Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Funktionen einer Veränderlichen - Potenzen und Logarithmen

Vereinfachung arithmetischer Ausdrücke in Maple

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Zur Vereinfachung kann auch Maple verwendet werden:
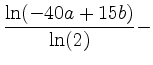Soll der Ausdruck

$\displaystyle \frac{\ln(-40a+15b)}{\ln(2)}-$ld$\displaystyle (-16a+6b) $

vereinfacht werden, so lauten die Eingaben in Maple
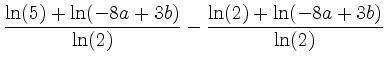
> simplify(ln(-40*a+15*b)/ln(2)-log[2](-16*a+6*b), ln);

$\displaystyle \frac{\ln(5)+\ln(-8a+3b)}{\ln(2)}-\frac{\ln(2)+\ln(-8a+3b)}{\ln(2)} $

> simplify(%);

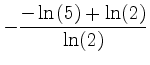
$\displaystyle -\frac{-\ln(5)+\ln(2)}{\ln(2)} $

Das erste simplify(expr,ln) vereinfacht den Ausdruck expr nach dem natürlichen Logarithmus. Der zweite Aufruf von simplify mit dem Argument % vereinfacht den letzten Term weiter.
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017