Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Konvergenz und Grenzwerte - Folgen

Rechenregeln für Grenzwerte bei Folgen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Für konvergente Folgen $ (a_n)$ und $ (b_n)$ mit Grenzwerten $ a$ und $ b$ gilt:

Summe und Differenz: Aus der Dreiecksungleichung folgt

$\displaystyle \vert (a_n \pm b_n) -(a\pm b)\vert \leq \vert a_n - a \vert + \vert b_n -b \vert \rightarrow 0. $

Produkt: Da $ a_n$ beschränkt ist, folgt

$\displaystyle \vert a_nb_n -ab\vert = \vert a_nb_n -a_nb + a_n b - ab\vert \leq \vert a_n\vert \vert b_n -b\vert + \vert b\vert\vert a_n -a \vert \rightarrow 0. $

Quotient: Für $ n>n_0$ ist

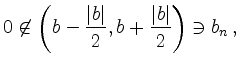
$\displaystyle 0 \not \in \left( b-\frac{\vert b\vert}{2},b+\frac{\vert b\vert}{2} \right)\ni b_n\,, $

und es folgt

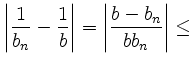$\displaystyle \left\vert\frac{1}{b_n}- \frac{1}{b}\right\vert = \left\vert \frac{b-b_n}{bb_n}\right\vert\leq$    const $\displaystyle \vert b_n - b\vert \rightarrow 0,$

d.h. $ 1/b_n\rightarrow 1/b$ . Die Konvergenz von $ a_n/b_n$ folgt nun aus der bereits bewiesenen Regel für Produkte konvergenter Folgen.

(Autoren: App/Höllig )
Sind die Folgenelemente rationale Funktionen von $ n$, $ a_n = \frac{p(n)}{q(n)}$, so lässt sich der Grenzwert nach Kürzen durch die höchste Potenz ermitteln. Beispielsweise ist

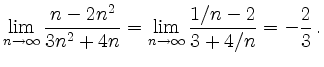
$\displaystyle \lim_{n\rightarrow\infty}\frac{n-2n^2}{3n^2+4n} = \lim_{n\rightarrow\infty} \frac{1/n-2}{3+4/n}=-\frac{2}{3} \,. $

Allgemein gilt für Zähler-Grad $ j$ und Nenner-Grad $ k$

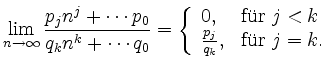
$\displaystyle \lim_{n\rightarrow\infty} \frac{p_j n^j+\cdots p_0}{q_k n^k+\cdot... ...\text{f''ur } j<k \\ \frac{p_j}{q_k}, & \text{f''ur } j=k. \end{array} \right. $

Für $ j>k$ divergiert die Folge.

(Autoren: App/Höllig )
Mit Hilfe der bekannten Grenzwerte

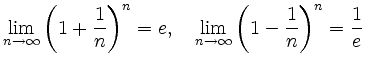
$\displaystyle \lim_{n\rightarrow\infty}\left( 1+\frac{1}{n} \right)^n=e, \quad \lim_{n\rightarrow\infty}\left( 1-\frac{1}{n} \right)^n=\frac{1}{e} $

folgt

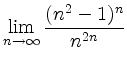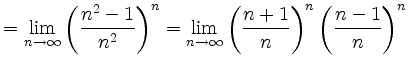$\displaystyle \lim_{n\rightarrow\infty}\frac{(n^2-1)^n}{n^{2n}}$ $\displaystyle = \lim_{n\rightarrow\infty}{\left(\frac{n^2-1}{n^2}\right)^n} = \... ...{n\rightarrow\infty}{\left(\frac{n+1}{n}\right)^n \left(\frac{n-1}{n}\right)^n}$    
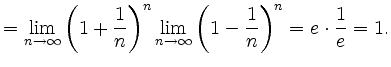  $\displaystyle = \lim_{n\rightarrow\infty}{\left(1+\frac{1}{n}\right)^n \lim_{n\rightarrow\infty} \left(1-\frac{1}{n}\right)^n} = e\cdot\frac{1}{e}=1.$    

Man berücksichtige, daß

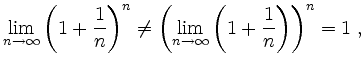
$\displaystyle \lim_{n\rightarrow\infty}\left( 1+\frac{1}{n} \right)^n\neq \left( \lim_{n\rightarrow\infty} \left(1+\frac{1}{n}\right) \right)^n=1 \; , $

da die Anzahl der Faktoren des Produktes nicht konstant sind.
(Autoren: Höllig/Kreitz )
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017