Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Konvergenz und Grenzwerte - Folgen

Cauchy-Kriterium

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Eine Folge $ (a_n)$ konvergiert genau dann, wenn für alle $ \varepsilon > 0 $ ein $ n_{\varepsilon}$ existiert, so dass

$\displaystyle \vert a_j - a_k \vert < \varepsilon $

für alle $ j,k > n_\varepsilon$ .

Mit Hilfe dieses auf Cauchy zurückgehende Kriteriums ist der Nachweis der Konvergenz ohne Kenntnis des Grenzwertes möglich.

Die Notwendigkeit des Cauchy-Kriteriums folgt aus der Definition des Grenzwerts:

$\displaystyle a=\lim a_n \ \Longleftrightarrow \ \vert a_m - a \vert < \varepsilon$    für $\displaystyle m > m_\varepsilon $

Setzt man $ n_\varepsilon=m_{\varepsilon /2}$ , so gilt

$\displaystyle \vert a_j - a_k \vert \leq \vert a_j - a \vert + \vert a - a_k \vert < \varepsilon /2 + \varepsilon /2 = \varepsilon $

für $ j, k > n_\varepsilon$ , wie behauptet.

Dass die Bedingung auch hinreichend ist, ist schwieriger zu zeigen, und beruht auf der Vollständigkeit der reellen Zahlen.

(Autoren: App/Höllig )
Bei rekursiv definierten Folgen $ (a_n)$ läßt sich das Cauchy-Kriterium oft durch Nachweis der Abschätzung

$\displaystyle \vert a_{n+1} - a_{n}\vert \leq cq^n$

mit $ q \in [0, 1)$ verifizieren. Diese sogenannte geometrische Konvergenz impliziert für $ j < k$

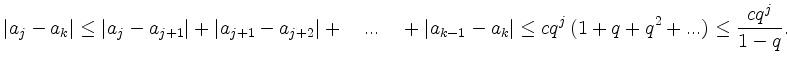
$\displaystyle \vert a_j - a_k\vert \leq \vert a_j - a_{j+1}\vert + \vert a_{j+1... ...uad + \vert a_{k-1} - a_k\vert \leq cq^j\,(1+q+q^2+...) \leq \frac{cq^j}{1-q}. $

Die rechte Seite ist für $ < \varepsilon$ für $ j, k > n_{\varepsilon} = \ln\frac{\varepsilon(1-q)}{c}/\ln q$, das Cauchy-Kriterium also erfüllt.

Für die konkrete, durch

$\displaystyle a_n = \sqrt{2 + a_{n-1}},\quad a_0 = 1, $

rekursiv definierte Folge $ a_n$ verwendet man zum Nachweis der geometrischen Konvergenz Induktion.

Induktionsanfang $ (n=1):$ Die Ungleichung

$\displaystyle \vert a_1 - a_0\vert \leq cq $

gilt, wenn $ c = \vert a_1 - a_0\vert/q$ gesetzt wird.

Induktionsschluss $ (n \rightarrow n+1)$: Man schreibt die abzuschätzende Differenz in der Form

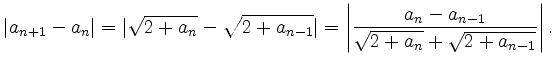
$\displaystyle \vert a_{n+1} - a_n\vert = \vert\sqrt{2 + a_{n}} - \sqrt{2 + a_{n... ...\vert \frac{a_n - a_{n-1}}{\sqrt{2 + a_{n}} + \sqrt{2 + a_{n-1}}} \right\vert. $

Nach Induktions-Voraussetzung ist die rechte Seite $ \leq \frac{1}{2\sqrt{2}}cq^n$ und mit der Wahl $ q = 1/2\sqrt{2}$ $ \leq$ $ cq^{n+1}$ wie gewünscht.
(Autoren: Höllig/Kreitz )
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017