Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Konvergenz und Grenzwerte - Folgen

Rekursive Approximation von Pi

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die halben Längen $ a_{\mathit n}$ und $ b_{\mathit n}$ der um- und einbeschriebenen $ \left(6\cdot 2^{\mathit n}\right)$ -Ecke eines Einheitskreises genügen der Rekursion

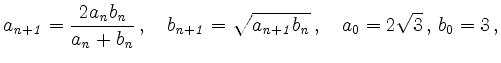
$\displaystyle a_{\mathit{n+1}} = \frac{2a_{\mathit n}b_{\mathit n}}{a_{\mathit... ...1}} = \sqrt{a_{\mathit{n+1}}b_{\mathit n}}\,,\quad a_0=2\sqrt{3}\,,\,b_0=3\,, $

mit deren Hilfe $ \pi = 3.1415926535897932 \ldots$ approximiert werden kann.

Diese Formeln wurden von Johann Friedrich Pfaff (1765-1825) im Jahr 1800 gefunden.

Archimedes (287-212 v. Chr.) hat mit Hilfe des 96-Ecks ($ n=4$ ) und der Abschätzung $ \frac{265}{153} < \sqrt{3}$ die Relation

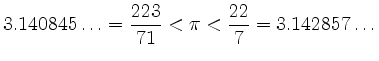
$\displaystyle 3.140845 \ldots =\frac{223}{71} < \pi < \frac{22}{7} = 3.142857\ldots $

gewonnen.

(Inhalt vorübergehend nicht verfügbar)

(Inhalt vorübergehend nicht verfügbar)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017