Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Funktionen einer Veränderlichen - Grundlagen

Gerade und ungerade Funktionen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Eine Funktion $ f$ ist gerade, wenn $ f(x) = f(-x)$ , d.h., wenn der Graph symmetrisch zur $ y$ -Achse ist. Für eine ungerade Funktion ist $ f(x) = -f(-x)$ , und der Graph ist punktsymmetrisch zum Ursprung.
\includegraphics[width=6.5cm]{Gerade_Funktion_Bild1}   \includegraphics[width=6.5cm]{Ungerade_Funktion_Bild1}
Das Produkt zweier gerader oder ungerader Funktionen ist gerade. Hingegen ist das Produkt einer geraden und einer ungeraden Funktion ungerade. Beim Bilden von Summen oder Differenzen bleibt der Typ erhalten.

Die folgende Abbildung zeigt links einige gerade und rechts einige ungerade Funktionen.
\includegraphics[width=.42\linewidth]{Gerade_Bsp}   \includegraphics[width=.42\linewidth]{Ungerade_Bsp}
Durch Bilden geeigneter Kombinationen erhält man weitere Beispiele. So sind die Funktionen

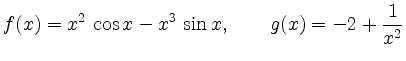
$\displaystyle f(x)=x^2\, \cos x-x^3\, \sin x,\hspace{2em} g(x)=-2+\frac{1}{x^2} $

gerade und

$\displaystyle h(x)=f(x)\sin x -g(x) x^3 $

ist ungerade.
(Autoren: Höllig/Hörner/Knesch)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017