Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Funktionen einer Veränderlichen - Grundlagen

Monotone Funktion

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Eine Funktion $ f$ ist auf einem Intervall D (strikt) monoton wachsend, wenn

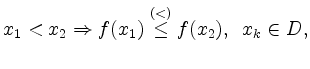
$\displaystyle x_1 < x_2 \Rightarrow f(x_1) \stackrel{(<)}{\leq} f(x_2), \,\,\, x_k \in D, $

bzw., falls $ f$ stückweise stetig differenzierbar ist, wenn

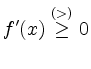
$\displaystyle f'(x) \stackrel{(>)}{\geq} 0$

für alle $ x \in D$ bis auf isolierte Punkte.

\includegraphics[bb=139 614 405 729,clip,width=.6\linewidth]{monoton_wachsend_Bild}

Analog definiert man (strikt) monoton fallend.

Die Funktion $ x\mapsto f(x)=\frac{1}{3}(x-2)^2(x+1)$ hat an der Stelle $ x=0$ einen Hochpunkt ( $ f'(0)=0, f''(0)<0$) und an der Stelle $ x=2$ einen Tiefpunkt ( $ f'(2)=0, f''(2)>0$). Für $ x\leq0$ und $ x\geq2$ ist die Funktion strikt monoton steigend und für $ 0 \leq x \leq 2$ strikt monoton fallend.

\includegraphics[width=.45\linewidth]{monotonie}
(Autoren: Höllig/Hörner/Knesch)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017