Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Konvergenz und Grenzwerte - Stetigkeit

Extrema stetiger Funktionen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Eine stetige Funktion hat auf einem endlichen abgeschlossenen Intervall $ [a,b]$ mindestens ein Minimum und Maximum.

\includegraphics[width=.6\linewidth]{Extrema_stet_Fkt.eps}

Es gibt ein $ c>0$ mit

$\displaystyle (x+y)^n \leq c(x^n + y^n)$

für $ x,y \geq 0$.

Zum Beweis setzt man für $ x\neq 0$ (der Fall $ x=0$ ist trivial),

$\displaystyle z= y/x $

und betrachtet die stetige Funktion

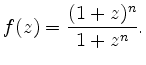
$\displaystyle f(z) = \frac{(1+z)^n}{1+z^n}.$

Da $ \lim\limits_{z\rightarrow\infty} f(z) = 1$ ist, existiert ein $ b>0$, so dass $ f(z) \leq 2 $ für $ z \geq b$ gilt. Mit

$\displaystyle c=\max\left\{2, \max_{z\in [0,b]}f(z)\right\} $

folgt

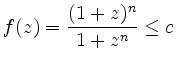
$\displaystyle f(z)=\frac{(1+z)^n}{1+z^n}\leq c$

und damit obige Behauptung.

(Autoren: App/Höllig )
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017