Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Konvergenz und Grenzwerte - Folgen und Reihen von Funktionen

Konvergenz von Funktionenreihen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
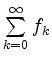Eine Reihe $ \sum\limits_{k=0}^\infty f_k$ von Funktionen 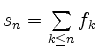$ f_k$ ist punktweise (gleichmäßig) konvergent, wenn dies für die Folge der Partialsummen $ s_n=\sum\limits_{k\le n} f_k$ der Fall ist.

Eine Verschärfung ist absolute Konvergenz, bei der gleichmäßige Konvergenz von $ \sum\limits_n \vert f_n\vert$ gefordert wird. In diesem Fall bleibt die Konvergenz auch bei einer beliebigen Umordnung der Reihe erhalten.

Definitionsgemäß übertragen sich die Aussagen über Funktionenfolgen.

(Inhalt vorübergehend nicht verfügbar)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017