Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Differentiation - Ableitungsregeln

Implizites Differenzieren

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Ist eine Funktion $ y=f(x)$ implizit, d.h. durch eine Gleichung in $ x$ und $ y$ gegeben, so kann man beide Seiten dieser Gleichung unmittelbar nach $ x$ differenzieren. Dabei ist lediglich bei den Ausdrücken in $ y=y(x)$ die Kettenregel anzuwenden.

Beispielsweise erhält man für die durch

$\displaystyle E: \; x^2+3y^2=7 $

gegebene Ellipse

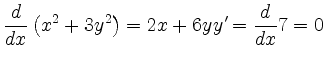
$\displaystyle \frac{d}{dx}\left( x^2+3y^2 \right)=2x+6yy'=\frac{d}{dx}7=0 $

bzw.

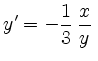$\displaystyle y'=-\frac{1}{3}\,\frac{x}{y} \:$.$\displaystyle $

Damit kann die Steigung der Tangente in einem Punkt auf $ E$ mit $ y\neq 0$ bestimmt werden. Beispielsweise erhält man für $ (2,1)$

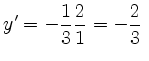$\displaystyle y'=-\frac{1}{3}\frac{2}{1}=-\frac{2}{3} \:$.$\displaystyle $

\includegraphics[width=8cm]{bsp_Kettenregel2_bild_1.eps}

Analog berechnen sich höhere Ableitungen. Unter Verwendung der Produktregel für $ yy'$ ist

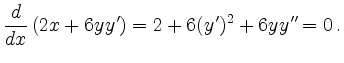
$\displaystyle \frac{d}{dx}\left( 2x +6yy' \right)=2+6(y')^2+6yy''=0 \,. $

Hieraus folgt

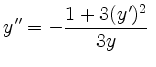$\displaystyle y''=-\frac{1+3(y')^2}{3y}\:$.$\displaystyle $

Wiederum kann man durch Einsetzen der Koordinaten eines Punktes auf $ E$ und des bereits bestimmten Wertes von $ y'(x)$ konkrete Werte bestimmen.
(Autoren: Höllig/Kopf)

(Inhalt vorübergehend nicht verfügbar)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017