Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Differentiation - Ableitungsregeln

Ableitung der Umkehrfunktion

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Ist eine Funktion $ y=f(x)$ stetig differenzierbar mit $ f'(x)\ne 0$ , so ist $ f$ in einer Umgebung von $ x$ invertierbar, und es gilt

$\displaystyle (f^{-1})'(y) = f'(x)^{-1}, $

bzw. $ dx/dy = (dy/dx)^{-1}$ .

\includegraphics[width=.6\linewidth]{Abl_Umkehrfunktion.eps}

Wie in der Abbildung veranschaulicht, sind die Steigungen von $ f$ und $ f^{-1}$ reziprok.

Setzt man $ g=f^{-1}$ , so erhält man

$\displaystyle x = g(f(x))$

und nach Differentiation mit der Kettenregel

$\displaystyle 1 = g'(f(x))f'(x)\,.$

Mit $ y=f(x)$ folgt die Behauptung.

\includegraphics[width=.6\linewidth]{Umkehrfunktion_1.eps}

Daß die Steigungen von $ f$ und $ f^{-1}$ an ensprechenden Stellen $ x$ und $ y$ reziprok zueinander sind, wird auch klar, wenn man berücksichtigt, dass $ f$ und $ f^{-1}$ symmetrisch zur ersten Winkelhalbierenden sind.

(Autoren: App/Höllig )
Um die Ableitung der Umkehrfunktion $ x = \arctan y$ der Tangensfunktion zu bestimmen, berechnet man zunächst

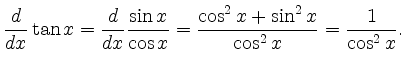$\displaystyle \frac{d}{dx} \tan x = \frac{d}{dx} \frac{\sin x}{\cos x} = \frac{\cos^2 x + \sin^2 x}{\cos^2 x} = \frac{1}{\cos^2 x}.$    

Damit folgt

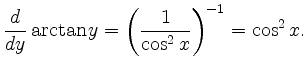$\displaystyle \frac{d}{dy} \arctan y = \left(\frac{1}{\cos^2 x}\right)^{-1} = \cos^2 x.$    

\includegraphics[height=4.5cm]{arctan_1.eps}   \includegraphics[height=4.5cm]{arccot_1.eps}
Die rechte Seite muss nun als Funktion von $ y$ geschrieben werden. Dazu verwendet man die Identität

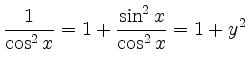$\displaystyle \frac{1}{\cos^2 x} = 1 + \frac{\sin^2 x}{\cos^2 x} = 1 + y^2$    

und erhält

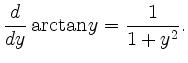$\displaystyle \frac{d}{dy} \arctan y = \frac{1}{1 + y^2}.$    

Analog zeigt man für die Umkehrfunktion des Kotangens,

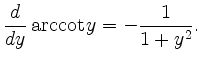$\displaystyle \frac{d}{dy} \operatorname{arccot} y = -\frac{1}{1 + y^2}.$    

(Autoren: App/Höllig )
Die Funktion

$\displaystyle y = f(x) = x\,(1-x) $

besitzt auf den Intervallen $ (-\infty,1/2]$ und $ [1/2, \infty)$ jeweils eine Umkehrfunktion $ x = g(y)$ .
\includegraphics[width=0.5\linewidth]{a_umkehrfunktion_1.eps}
In beiden Fällen gilt

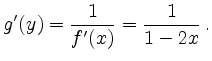
$\displaystyle g'(y) = \frac{1}{f'(x)} = \frac{1}{1-2x}\,. $

Nochmaliges Differenzieren ergibt

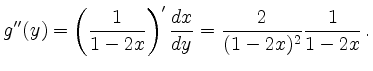
$\displaystyle g''(y) = \left( \frac{1}{1-2x}\right)' \frac{dx}{dy} = \frac{2}{(1-2x)^2} \frac{1}{1-2x}\,. $

Speziell erhält man für $ x = 1, y = 0$

$\displaystyle g'(0) = 1 ,\quad g''(0) = -2\,. $

Die Ableitungen sind also berechenbar, ohne dass die Umkehrfunktion explizit gebildet werden muss. Dies ist nur dann möglich, wenn man $ g'(y)$ als Funktion von $ y$ schreiben kann. In diesem Beispiel ist das möglich, denn $ x$ lässt sich als Funktion von $ y$ schreiben:

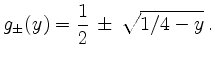
$\displaystyle g_{\pm}(y) = \frac{1}{2}\,\pm\,\sqrt{1/4 - y}\,. $

Die obigen Werte können so überprüft werden, wobei der dem Wertepaar $ (1, 0)$ entsprechende Zweig gewählt werden muss.

(Autoren: Höllig/Kreitz )
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017