Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Differentiation - Anwendungen

Logarithmische Ableitung

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die Formel

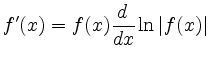
$\displaystyle f'(x) = f(x) \frac{d}{dx}\ln\vert f(x)\vert $

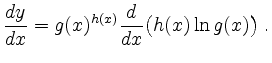
kann zur Differentiation von Funktionen der Form $ y = g(x)^{h(x)}$ mit $ g(x)>0$ benutzt werden. Man erhält

$\displaystyle \frac{d y}{dx}=g(x)^{h(x)}\frac{d}{dx}\big( h(x) \ln g(x) \big) \;. $

Für die Funktion

$\displaystyle f(x)=x^x$

mit $ x>0$ ist die Ableitung

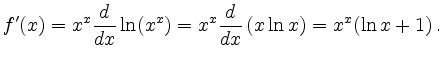
$\displaystyle f'(x)=x^x\frac{d}{dx}\ln(x^x)= x^x \frac{d}{dx}\,( x\ln x) = x^x(\ln x +1)\,.$

\includegraphics[height=.45\moimageheight]{a_log_ableit.eps}

Für $ x \rightarrow 0$ strebt $ \ln\,f(x) = x\,\ln\,x$ gegen 0, also $ x^x$ gegen $ e^0 = 1$ . Die Funktion ist also bei Null rechtsseitig stetig. Für die Ableitung ist dies nicht der Fall. Wegen $ x^x \rightarrow 1$ und $ \ln\,x + 1 \rightarrow -\infty$ für $ x \rightarrow 0$ hat $ f$ eine senkrechte Tangente bei Null.

(Autoren: App/Höllig )
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017