Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Differentiation - Anwendungen

Fehlerfortpflanzung

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Bezeichnet $ \Delta x = \tilde x -x$ den absoluten Fehler eines Messwerts oder einer Näherung $ \tilde x\approx x$ so gilt für eine stetig differenzierbare Funktion $ f$

$\displaystyle \vert \Delta y \vert = \vert f'(x)\vert \vert\Delta x\vert + o(\Delta x) $

mit $ \Delta y=f(\tilde x) - f(x)$. Entsprechend gilt für den relativen Fehler

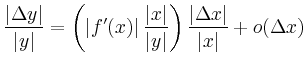
$\displaystyle \frac{\vert\Delta y\vert}{\vert y\vert} = \left( \vert f'(x)\vert... ...ert}{\vert y\vert} \right) \frac{\vert\Delta x\vert}{\vert x\vert}+o(\Delta x) $

falls $ x,y\neq 0$. Der Ausdruck in Klammern wird als Konditionszahl $ c_r$ von $ f$ an der Stelle $ x$ bezeichnet.

Durch Vernachlässigung des Terms $ o(\Delta x)$ lässt sich die Verstärkung des Fehlers näherungsweise abschätzen. Dabei können statt exakter Ableitungswerte auch geeignete Schranken verwendet werden:

$\displaystyle \vert \Delta y\vert \leq c_a \vert \Delta x\vert\,, \quad c_a \geq \max_{\vert t-x\vert \leq \vert \Delta x\vert} \vert f'(t)\vert\,. $

Entsprechend ist $ c_r = c_a \frac{\vert x\vert}{\vert y\vert}$ eine Schranke für die Verstärkung des relativen Fehlers.

(Inhalt vorübergehend nicht verfügbar)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017