Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Differentiation - Anwendungen

Newton-Verfahren

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Mit dem Newton-Verfahren kann eine Nullstelle $ x_\ast$ einer Funktion $ f$ numerisch bestimmt werden. Dabei wird durch Linearisierung eine Folge $ x_0,\,x_1\,\ldots$ von Approximationen für $ x_\ast$ generiert. Die Näherung $ x_{\ell+1}$ ist der Schnittpunkt der Tangente im Punkt $ \left( x_\ell,f(x_\ell) \right)$ mit der $ x$-Achse:

$\displaystyle x_{\ell+1} = x_\ell - f(x_\ell)/f^\prime(x_\ell)$

\includegraphics[width=0.4\linewidth]{Newton_Verfahren}

Für eine einfache Nullstelle $ x_\ast$ ( $ f^\prime(x_\ast)\neq 0$) konvergiert die Newton-Iteration lokal quadratisch, d.h.

$\displaystyle \left\vert x_{\ell+1}-x_{\ast} \right\vert \leq c\; \left\vert x_{\ell}-x_{\ast} \right\vert^2 $

für Startpunkte $ x_0$ in einer hinreichend kleinen Umgebung von $ x_\ast$.

Durch lineare Taylor-Approximation erhält man

$\displaystyle 0=f(x_\ast)=f(x_\ell)+f'(x_\ell)(x_\ast-x_\ell)+R $

mit dem Restglied

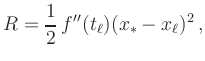
$\displaystyle R=\frac{1}{2}\,f''(t_\ell)(x_\ast-x_\ell)^2\,, $

für ein $ t_\ell$ zwischen $ x_\ast$ und $ x_\ell$. Setzt man

$\displaystyle f(x_\ell)=f'(x_\ell)(x_\ell-x_\ast)-R $

in die Iterationsvorschrift ein, so folgt

$\displaystyle x_{\ell+1} = x_\ast + R/f'(x_\ell)\,. $

Für $ f^{'}(x_\ell) \neq 0$ gilt also

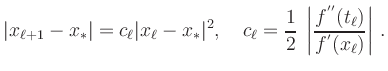
$\displaystyle \vert x_{\ell+1} - x_{\ast}\vert = c_\ell\vert x_\ell - x_{\ast}\... ... = \frac{1}{2}\;\left\vert \frac{f^{''}(t_\ell)}{f^{'}(x_\ell)} \right\vert\,. $

Gilt $ f^{'}(x_{\ast}) \neq 0$, so ist $ c_\ell$ aus Stetigkeitsgründen für $ x_\ell$ in einer Umgebung $ [x_{\ast} - \delta, x_{\ast} + \delta]$ von $ x_{\ast}$ beschränkt:

$\displaystyle c_\ell \leq c\,. $

Damit folgt die quadratische Konvergenz.

(Inhalt vorübergehend nicht verfügbar)
Die schon von den Babyloniern verwendete Iteration

$\displaystyle x \longleftarrow (x+a/x)/2$

zur Berechnung der Wurzel einer positiven Zahl $ a$ stellt sich bei genauerer Betrachtung als das Newton-Verfahren für $ f(x)=x^2-a$ heraus:

$\displaystyle \frac{1}{2}\left(x+\frac{a}{x}\right)=x-\frac{x^2-a}{2x} $

Für $ a=2, x_0=1$ erhält man die Approximationen
1
1.5
1.416666666666666666666666666666666666667
1.414215686274509803921568627450980392157
1.414213562374689910626295578890134910117
1.414213562373095048801689623502530243615
1.414213562373095048801688724209698078570

Die Konvergenz ist äußerst schnell. Bei jedem Schritt verdoppelt sich die Anzahl der korrekten Stellen (unterstrichen) annähernd. Die quadratische Konvergenz lässt sich in diesem Beispiel auch durch einfache Umformung nachweisen:

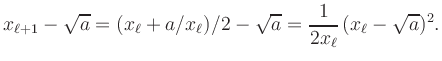
$\displaystyle x_{\ell+1}-\sqrt{a} = (x_\ell+a/x_\ell)/2-\sqrt{a} = \frac{1}{2x_\ell}\,(x_\ell-\sqrt{a})^2. $

Die geometrische Interpretation des Newton-Verfahrens zeigt, dass die Iteration für alle $ x_0 \neq 0$ konvergent ist.

Die Abbildung illustriert die Konvergenz der komplexen Newton-Iteration für die Gleichung

$\displaystyle z^3 - 1 = 0 $

mit den Lösungen $ z=\exp(2\pi$i$ k/3)$, $ k=0,1,2$. Die verschiedenen Farben kennzeichnen die Konvergenzgebiete für die jeweiligen Nullstellen. Dunklere Farbtöne entsprechen dabei schnellerer Konvergenz.

\includegraphics[width=\moimagesize]{z3color}

Man erkennt deutlich den fraktalen Charakter der Ränder der Konvergenzgebiete.

(Autoren: App/Höllig )
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017