Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Lineare Algebra - Normalformen - Singulärwertzerlegung

Pseudo-Inverse

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Mit der Singulärwert-Zerlegung $ USV^*$ einer komplexen $ (m\times n)$-Matrix $ A$ lässt sich die Lösung des Ausgleichsproblems $ \vert Ax-b\vert\to\min$ mit minimaler Norm in der Form

$\displaystyle x = A^+b,\quad A^+ = VS^+U^*, $

schreiben, wobei $ A^+$ als Pseudo-Inverse von $ A$ bezeichnet wird, und

$\displaystyle S^+ = \operatorname{diag}(1/s_1,\ldots,1/s_k,0,\ldots,0), \quad k = \operatorname{Rang} A \,, $

die $ (n \times m)$-Diagonalmatrix mit den Kehrwerten der positiven singulären Werte ist.

Bezeichnen $ \{u_1,\ldots,u_m\}$ und $ \{v_1,\ldots,v_n\}$ die orthonormalen Basen aus den Spalten von $ U$ bzw. $ V$, so lässt sich die lineare Abbildung $ b\mapsto x= A^+b$ in der faktorisierten Form

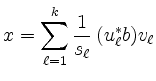
$\displaystyle x = \sum_{\ell=1}^k \frac{1}{s_\ell}\,(u^*_\ell b)v_\ell $

darstellen. Daraus folgt insbesondere, dass

$\displaystyle \operatorname{Kern}A^+ = \operatorname{span} \{u_{k+1},\ldots,u_m\},\quad \operatorname{Bild}A^+ = \operatorname{span} \{v_1,\ldots,v_k\} $

und $ \Vert A^+\Vert _2 = 1/s_k$.

(Inhalt vorübergehend nicht verfügbar)

(Inhalt vorübergehend nicht verfügbar)
Zur Kontrolle topographischer Höhendaten $ h_i$ werden Höhendifferenzen $ d_{i,j}$ gemessen. Aufgrund von Messfehlern gilt in der Regel $ d_{i,j}\neq h_i-h_j$. Geeignete Höhenkorrekturen $ x_i$ lassen sich durch Lösen des Ausgleichsproblems

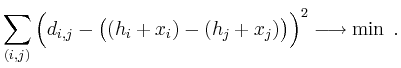
$\displaystyle \sum_{(i,j)}\Big(d_{i,j}-\big( (h_i+x_i)-(h_j+x_j) \big) \Big)^2 \longrightarrow \min \; . $

Zur Illustration der Vorgehensweise wird ein Modellproblem mit wenigen Daten gelöst.

\includegraphics[width=.7\linewidth]{topo.eps}
Für die Höhen und Differenzwerte

$\displaystyle h=(834, 561, 207, 9)^{\operatorname t}, \quad d=(276, 631, 822, 356, 549)^{\operatorname t} $

mit $ d=(d_{1,2}, d_{1,3}, d_{1,4}, d_{2,3}, d_{2,4})^{\operatorname t}$, erhält man das überbestimmte System

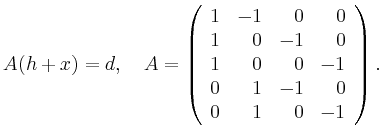
$\displaystyle A(h+x)=d, \quad A= \left(\begin{array}{rrrr} 1 & -1 & 0 & 0 \\ 1... ... 0 \\ 1 & 0 & 0 & -1 \\ 0 & 1 & -1 & 0 \\ 0 & 1 & 0 & -1 \end{array} \right). $

Die gesuchte Lösung minimaler Norm ist dann

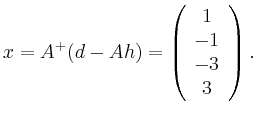
$\displaystyle x = A^+ (d - Ah) = \left( \begin{array}{c} 1 \\ -1 \\ -3 \\ 3 \end{array} \right). $

Die Berechnung der Minimum-Norm-Lösung ist für die betrachtete Anwendung sinnvoll, denn es soll eine möglichst kleine Korrektur bestimmt werden.
(Autor: Wipper)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 14.6.2012