Mathematik-Online-Kurs: Lineare Algebra-Lineare Gleichungssysteme-Direkte Methoden-Lösung eines linearen Gleichungssystems in Zeilenstufenform

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Kurs: Lineare Algebra - Lineare Gleichungssysteme - Direkte Methoden
	Lösung eines linearen Gleichungssystems in Zeilenstufenform

[vorangehende Seite] [nachfolgende Seite]

[Gesamtverzeichnis][Seitenübersicht]

Ein lineares Gleichungssystem

in Zeilenstufenform,

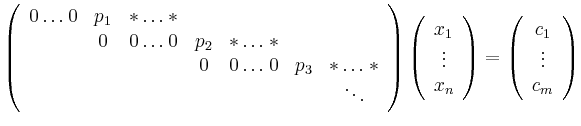
$\displaystyle \left(\begin{array}{cccc ccc} 0\ldots0 & p_1 & *\ldots* \\ & 0 &... ...rray}\right) = \left(\begin{array}{c} c_1 \\ \vdots \\ c_m \end{array}\right)$

mit Pivots $p_1,\ldots,p_k$ ist genau dann lösbar, wenn $c_{k+1}=\cdots=c_m=0$ . Die Lösung ist eindeutig, falls

. Für

gibt es

linear unabhängige Lösungen des homogenen linearen Gleichungssystems (

). Die Unbekannten, die den Spalten ohne Pivots entsprechen, können frei gewählt werden.

Im Folgenden werden mehrere typische Fälle diskutiert.

$\displaystyle \left(\begin{array}{rrrr} 1&5&0&3\\ 0&4&-1&3\\ 0&0&-2&7\\ 0... ..._4\end{array}\right)= \left(\begin{array}{r} -1\\ 0\\ 9\\ 1 \end{array}\right)$
Durch Rückwärts-Einsetzen erhält man rekursiv die eindeutige Lösung

$\displaystyle x=(1,-1,-1,1)^{\operatorname t}.$
, $c_4\ne 0$

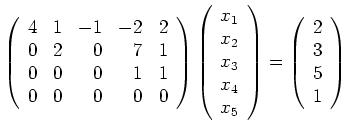
$\displaystyle \left(\begin{array}{rrrrr} 4&1&-1&-2&2\\ 0&2&0&7&1\\ 0&0&0&1... ... x_5\end{array}\right)= \left(\begin{array}{r}2\\ 3\\ 5\\ 1 \end{array}\right)$
In der letzten Zeile ergibt sich $0\cdot x=1$ , damit hat das lineare Gleichungssystem keine Lösung.
,

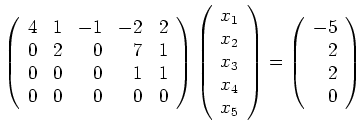
$\displaystyle \left(\begin{array}{rrrrr} 4&1&-1&-2&2\\ 0&2&0&7&1\\ 0&0&0&1... ...\\ x_5\end{array}\right)=\left(\begin{array}{r}-5\\ 2\\ 2\\ 0\end{array}\right)$
Da $c_{k+1}=0$ , ist das lineare Gleichungssystem lösbar. Wegen $\operatorname{Rang} D = 3 = n-2$ ist die Lösung jedoch nicht eindeutig. Es existieren 2 linear unabhängige Lösungen des homogenen Systems und die allgemeine Lösung hat die Form

$\displaystyle x = x_s + \alpha_1 v_1 + \alpha_2 v_2\,, \alpha_j \in \mathbb{R}$
mit einer speziellen Lösung des inhomogenen Systems.
Die Vektoren bestimmt man durch kanonische Wahl der nicht zu den Pivot-Spalten gehörigen Unbekannten und berechnet die restlichen Koeffizienten über das homogene System:

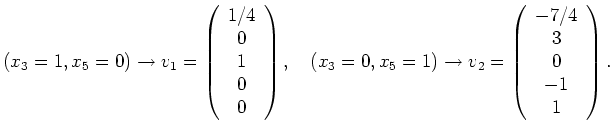
$\displaystyle (x_3=1, x_5=0) \rightarrow v_1=\left(\begin{array}{c} 1/4 \\ 0 \\... ...w v_2 = \left(\begin{array}{c} -7/4 \\ 3 \\ 0 \\ -1 \\ 1 \end{array} \right).$
Eine spezielle Lösung

$\displaystyle x_s = \left(\begin{array}{c} 5/4 \\ -6 \\ 0 \\ 2 \\ 0 \end{array} \right)$
erhält man durch Setzen von .

(Autoren: Höllig/Streit)

[vorangehende Seite] [nachfolgende Seite]

[Gesamtverzeichnis][Seitenübersicht]

automatisch erstellt am 14.6.2012