Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Lineare Algebra - Lineare Gleichungssysteme - Ausgleichsprobleme

Ausgleichsgerade

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Eine Gerade

$\displaystyle p(t) = u + vt\, , $

die Daten $ (t_i,f_i)$, $ i=1,\ldots,n$, bestmöglichst approximiert, kann durch Minimierung der Fehlerquadratsumme

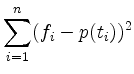
$\displaystyle \sum_{i=1}^n (f_i - p(t_i))^2 $

ermittelt werden.

\includegraphics[width=.7\moimagesize]{a_ausgleichsgerade}

Man erhält für den Achsenabschnitt $ u$ und die Steigung $ v$ die Formeln

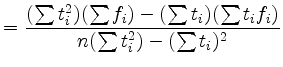$\displaystyle u$ $\displaystyle = \frac{(\sum t_i^2)(\sum f_i)-(\sum t_i)(\sum t_if_i)} {n(\sum t_i^2)-(\sum t_i)^2}$    
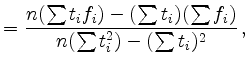$\displaystyle v$ $\displaystyle =\frac{n(\sum t_i f_i)-(\sum t_i)(\sum f_i)} {n(\sum t_i^2)-(\sum t_i)^2}\, ,$    

wenn mindestens zwei Abszissen $ t_i$ verschieden sind.

(Inhalt vorübergehend nicht verfügbar)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 14.6.2012