Mathematik-Online-Kurs: Repetitorium HM II-Lineare Algebra-Geometrie

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Kurs: Repetitorium HM II - Lineare Algebra
	Geometrie

[vorangehende Seite] [nachfolgende Seite]

[Gesamtverzeichnis][Seitenübersicht]

Sei der zugrundegelegte Körper $K=\mathbb{R}$ oder $K=\mathbb{C}$ . Sei $n\geq 1$ .

Orthogonalität.

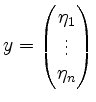Seien $x=\begin{pmatrix}\xi_1\\ \vdots\\ \xi_n\end{pmatrix}$ und $y=\begin{pmatrix}\eta_1\\ \vdots\\ \eta_n\end{pmatrix}$ Vektoren im .

Sei

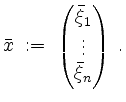
$\displaystyle \bar{x} \;:=\; \begin{pmatrix}\bar{\xi}_1\\ \vdots\\ \bar{\xi}_n\end{pmatrix}\;.$

Ist $K=\mathbb{R}$ , so ist $\bar{x}=x$ .

Das Skalarprodukt von und ist gegeben durch

$\displaystyle \bar{x}^\mathrm{t} y \;=\; \bar{\xi}_1 \eta_1 + \bar{\xi}_2 \eta_2 +\cdots+ \bar{\xi}_n \eta_n\;.$

Die Länge (oder auch Norm) von ist gegeben durch

$\displaystyle \Vert x\Vert \;=\; \sqrt{\bar{x}^\mathrm{t} x}\;.$

Der Vektor heißt normiert, falls $\Vert x\Vert=1$ .

Ist $x\ne 0$ , so schreiben wir

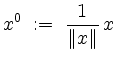
$\displaystyle x^0 \;:=\; \frac{1}{\Vert x\Vert}\,x$

für den normierten Vektor von

Die Cauchy-Schwarzsche Ungleichung schreibt sich nun

$\displaystyle \vert\bar{x}^\mathrm{t} y\vert \;\leq\; \Vert x\Vert\cdot\Vert y\Vert\;.$

Sind $x\ne 0$ und $y\ne 0$ , und ist $\varphi$ der von und eingeschlossene Winkel, so gilt

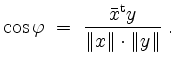
$\displaystyle \cos\varphi \;=\; \frac{\bar{x}^\mathrm{t} y}{\Vert x\Vert\cdot\Vert y\Vert}\;.$

Die Vektoren und heißen orthogonal, falls $\bar{x}^\mathrm{t} y=0$ . Im Falle $x\ne 0$ und $y\ne 0$ ist dies gleichbedeutend damit, daß der von und eingeschlossene Winkel gleich $\pm\pi/2$ ist.

Ein Tupel $(x_1,\ldots,x_m)$ von Vektoren in heißt orthonormal, falls und orthogonal sind für alle $j,k\in\{1,\ldots,m\}$ mit $j\ne k$ , und normiert ist für alle $j\in\{1,\ldots,m\}$ .

Ein orthonormales Tupel ist insbesondere linear unabhängig. Es ist dann eine Orthonormalbasis von $U := \langle x_1,\ldots,x_m\rangle\subseteq K^n$ .

Die orthogonale Projektion von auf ist gegeben durch

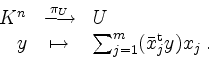
$\begin{displaymath} \begin{array}{rcl} K^n & \overset{\pi_U}\longrightarrow & U ... ... \sum_{j = 1}^m (\bar{x}^\mathrm{t}_j y)x_j\; . \\ \end{array}\end{displaymath}$

Der Abstand eines Punktes $y\in K^n$ zum Unterraum ist gegeben durch $\Vert y - \pi_U(y)\Vert$ .

Der von dem Vektor und dem Unterraum eingeschlossene Winkel ist gleich dem von den Vektoren und $\pi_U(y)$ eingeschlossenen Winkel, falls $\pi_U(y)\neq 0$ . Falls $\pi_U(y) = 0$ , so ist dieser Winkel gleich $\pm\pi/2$ - es steht orthogonal zu genau dann, wenn seine orthogonale Projektion auf verschwindet.

Gram-Schmidtsches Orthonormalisierungsverfahren.

Seien $x_1,\ldots,x_m\in K^n$ gegeben.

Das folgende Verfahren liefert eine Orthonormalbasis von $\langle x_1,\ldots,x_m\rangle$ .

Setze .

Sind $x_1',\ldots,x_k'$ bereits konstruiert für ein , so setze man

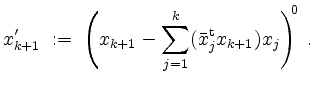
$\displaystyle x_{k+1}' \;:=\; \left(x_{k+1}-\sum_{j=1}^k (\bar{x}_j^\mathrm{t} x_{k+1})x_j\right)^{\!\!0}\;.$

Die Normierung werde nur dann durchgeführt, wenn der zu normierende Vektor $\ne 0$ ist. Ansonsten überspringe man den Vektor $x_{k+1}$ und fahre mit $x_{k+2}$ an seiner statt fort. Denn dann hat man $x_{k+1}\in\langle x_1,\dots,x_k\rangle$ nachgewiesen, und $x_{k+1}$ war als Erzeuger von redundant.

Als Resultat ist $(x_1',\ldots,x_l')$ eine Orthonormalbasis von $\langle x_1,\ldots,x_m\rangle$ . Es gilt genau dann, wenn $(x_1,\ldots,x_m)$ linear unabhängig ist.

Kreuzprodukt.

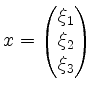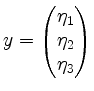Seien $x=\begin{pmatrix}\xi_1\\ \xi_2\\ \xi_3\end{pmatrix}$ und $y=\begin{pmatrix}\eta_1\\ \eta_2\\ \eta_3\end{pmatrix}$ Vektoren im $\mathbb{R}^3$ .

Das Kreuzprodukt von und ist definiert als

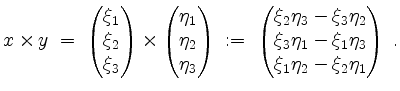
$\displaystyle x\times y \;=\; \begin{pmatrix}\xi_1\\ \xi_2\\ \xi_3\end{pmatrix}... ...xi_3\eta_2\\ \xi_3\eta_1-\xi_1\eta_3\\ \xi_1\eta_2-\xi_2\eta_1\end{pmatrix}\;.$

Der Vektor $x\times y$ ist orthogonal zu und zu . Seine Länge ist gleich dem Flächeninhalt des von und aufgespannten Parallelogramms. Insbesondere ist $x\times y=0$ genau dann, wenn linear abhängig ist.

Die Richtung von $x\times y$ kann man sich wie folgt veranschaulichen. Man wähle ein Koordinatensystem, in dem die $\xi_1$ -Achse in Richtung des Daumens der rechten Hand, die $\xi_2$ -Achse in Richtung des Zeigefingers und die $\xi_3$ -Achse in Richtung des Mittelfingers zeigt. Legt man nun den Daumen der rechten Hand in Richtung des Vektors und den Zeigefinger in Richtung des Vektors , so zeigt der Mittelfinger in Richtung des Kreuzproduktes $x\times y$ .

Es gelten folgende Regeln. Seien $x,\, y,\, z\,\in\,\mathbb{R}^3$ , und seien $\lambda,\,\lambda',\,\mu,\,\mu'\,\in\,\mathbb{R}$ .

$x\times y = -y\times x$ (Antikommutativität).
$(\lambda x + \lambda' x') \times (\mu y + \mu' y') = \lambda\mu (x\times y) + \lambda\mu' (x\times y') + \lambda'\mu (x'\times y) + \lambda'\mu' (x'\times y')$ (Bilinearität).
$(x\times y)\times z= (x^\mathrm{t} z)y-(y^\mathrm{t} z)x$ .

Hessesche Normalenform.

Sei $U\subseteq K^n$ ein Unterraum der Dimension , mit $1\leq m\leq n-1$ , und sei $x_0\in K^n$ . Wir wollen

$\displaystyle x_0 + U \;:=\; \{ x_0 + u\; \vert\; u\in U\} \;=\; \{x\in K^n\; \vert\; Ax = b\}$

mit einer geeigneten Matrix $A\in K^{(n - m)\times n}$ und einem geeigneten Vektor $b\in K^{n-m}$ schreiben, und zwar derart, daß die Spalten von $A^\mathrm{t}$ ein orthonormales Tupel bilden.

Sei hierzu $(x_1,\dots,x_m)$ eine Basis von , welche wir zu einer Basis $(x_1,\dots,x_m,x_{m+1},\dots,x_n)$ von ergänzen. Gram-Schmidt auf diese Basis angewandt liefert eine Orthonormalbasis $(x'_1,\dots,x'_m,x'_{m+1},\dots,x'_n)$ derart, daß $(x'_1,\dots,x'_m)$ eine Basis von darstellt. Sei nun $A\in K^{(n - m)\times n}$ die Matrix mit Zeilentupel $(\bar{x}'^{\mathrm{t}}_{m+1},\dots,\bar{x}'^{\mathrm{t}}_n)$ . Mit wird