Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Differentialrechnung mehrerer Veränderlicher - Stetigkeit

Banachscher Fixpunktsatz

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Ist $ g$ eine kontrahierende Abbildung, die eine nichtleere, abgeschlossene Menge $ D\subset\mathbb{R}^n$ in sich abbildet, d.h. gilt mit $ c<1$, dann besitzt $ g$ einen eindeutigen Fixpunkt $ x_*=g(x_*)\in D$. Ausgehend von $ x_0\in D$ kann $ x_\ast$ durch die Iterationsfolge

$\displaystyle x_0,\, x_1 = g(x_0),\, x_2=g(x_1),\,\ldots $

approximiert werden. Für den Fehler gilt

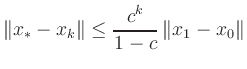
$\displaystyle \Vert x_*-x_k\Vert\le \frac{c^k}{1-c}\, \Vert x_1-x_0\Vert $

d.h. die Iterationsfolge konvergiert für jeden Startwert linear.

Der Fixpunktsatz gilt allgemein in vollständigen metrischen Räumen. Da die Translationsinvarianz und Homogenität der Norm nicht benötigt wird, kann man $ \Vert x-y\Vert$ durch eine allgemeine Abstandfunktion $ d(x,y)$ ersetzen.

Der Beweis gliedert sich in mehrere Teilschritte.

(i) Wegen $ g(D)\subseteq D$ ist $ x_\ell\in D$ für alle $ \ell>0$.

(ii) Aus der Kontraktionsbedingung folgt

$\displaystyle \Vert x_{\ell+1}-x_\ell\Vert = \Vert g(x_\ell)-g(x_{\ell-1})\Vert \le c\, \Vert x_\ell-x_{\ell-1}\Vert \,, $

und Iteration dieser Ungleichung führt auf

$\displaystyle \Vert x_{\ell+1}-x_\ell\Vert\le c^\ell\, \Vert x_1-x_0\Vert \,. $

(iii) Mit der Dreiecksungleichung erhält man

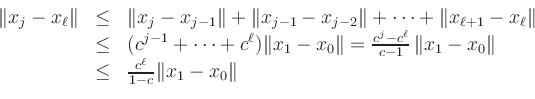
\begin{displaymath} \begin{array}{rcl} \Vert x_j-x_\ell\Vert&\le& \Vert x_j-x_{... ...ert \\ &\le& \frac{c^\ell}{1-c}\Vert x_1-x_0\Vert \end{array}\end{displaymath}

und damit die Cauchy-Konvergenz der Folge $ x_\ell$ gegen einen Grenzwert $ x_*$.

(iv) Wiederum aus der Kontraktionsbedingung folgt

$\displaystyle \Vert g(x_*)-x_*\Vert\le\Vert g(x_*)-g(x_j)\Vert+\Vert g(x_j)-x_*\Vert\le c\, \Vert x_*-x_{j}\Vert+\Vert x_{j+1}-x_*\Vert \,, $

und Bilden des Grenzwerts für $ j\to\infty$ zeigt, dass $ x_*$ ein Fixpunkt von $ g$ ist.

$ (v)$ Der Fixpunkt $ x_*$ ist eindeutig, da

$\displaystyle \Vert\tilde x_*-x_*\Vert= \Vert g(\tilde x_*)-g(x_*)\Vert\le c \Vert\tilde x_*-x_*\Vert $

mit $ c<1$.

(vi) Schließlich ergibt sich die Abschätzung für den Fehler durch Grenzübergang $ j\to\infty$ in der Ungleichung (iii) für $ \Vert x_j-x_\ell\Vert$.

Eine typische Anwendung des Banachschen Fixpunktsatzes ist ein gestörtes lineares System

$\displaystyle Ax + \varepsilon f(x) = b $

mit einer quadratischen invertierbaren Matrix $ A$ und Lipschitz-stetiger Funktion $ f$ (Konstante $ c_f$). Zur Bestimmung der Lösung wird die Iteration

$\displaystyle x \leftarrow g(x) = A^{-1}(b-\varepsilon f(x)) $

verwendet. Um die Konvergenz zu beweisen, verifiziert man die Voraussetzungen des Banachschen Fixpunktsatzes für die abgeschlossene Menge

$\displaystyle D=\{y:\ \Vert y-p\Vert\le r\},\quad p=A^{-1} b \,. $

(i)     
$ g(D)\subset D$: Für $ x\in D$ gilt

$\displaystyle \Vert g(x)-p\Vert = \varepsilon \Vert A^{-1}f(x)\Vert \le \varepsilon \Vert A^{-1}\Vert \max_{y\in D} \Vert f(y)\Vert \,.$

Damit liegt $ g(x)$ in $ D$ (Abstand zu $ p$ $ \le r$), falls

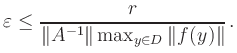
$\displaystyle \varepsilon \le \frac{r}{\Vert A^{-1}\Vert \max_{y\in D} \Vert f(y)\Vert} \,. $

(ii) Kontraktionsbedingung:
Die Abschätzung

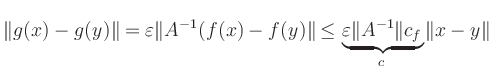
$\displaystyle \Vert g(x)-g(y)\Vert = \varepsilon \Vert A^{-1}(f(x)-f(y)\Vert \le \underbrace{\varepsilon \Vert A^{-1}\Vert c_f}_{c} \Vert x-y\Vert $

zeigt, dass $ g$ kontrahierend ist, falls $ c<1$, d.h. falls

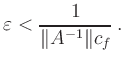
$\displaystyle \varepsilon < \frac{1}{\Vert A^{-1}\Vert c_f} \,. $

Beide Bedingungen ((i) und (ii)) sind für hinreichend kleines $ \varepsilon$ erfüllt.

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017