Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Differentialrechnung mehrerer Veränderlicher - Partielle Ableitungen

Partielle Ableitungen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die partielle Ableitung $ \partial_i f$ einer Funktion $ f$ nach der $ i$-ten Variablen $ x_i$ ist die Ableitung der univariaten Funktion

$\displaystyle x_i \mapsto f(x_1,\ldots,x_i,\ldots,x_n)\, , $

bei der die Variablen $ x_j$, $ j\ne i$, als Konstanten betrachtet werden. Man schreibt auch

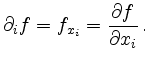
$\displaystyle \partial_i f = f_{x_i} = \frac{\partial f}{\partial x_i}\, . $

Gemäß der Definition der univariaten Ableitung gilt

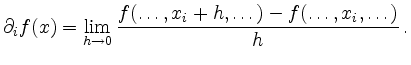
$\displaystyle \partial_i f(x) = \lim_{h\to0} \frac{f(\ldots,x_i+h,\ldots)-f(\ldots,x_i,\ldots)}{h} \,. $

Partielle Ableitungen sind sowohl für skalare als auch für vektorwertige reelle Funktionen definiert. In beiden Fällen bleibt der Funktionstyp beim partiellen Ableiten erhalten. Definitionsgemäß gilt

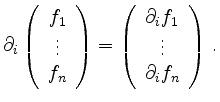
$\displaystyle \partial_i \left(\begin{array}{c} f_1 \\ \vdots \\ f_n \end{ar... ...{array}{c} \partial_i f_1 \\ \vdots \\ \partial_i f_n \end{array}\right)\, . $

Die partielle Ableitung wird simultan in den Komponenten gebildet.

Für die Definition der totalen Ableitung bzw. die lineare Approximation ist der Vektortyp von Bedeutung. Die übliche Konvention ist, sowohl für die Variable $ x$ als auch für die Funktion $ f$ Spaltenvektoren zu verwenden.

(Inhalt vorübergehend nicht verfügbar)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017