Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Differentialgleichungen - Spezielle skalare Differentialgleichungen - Differentialgleichungen zweiter Ordnung

Linearer Oszillator

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Die Auslenkung $ u(t)$ eines linearen Oszillators bei periodischer Anregung wird durch die Differentialgleichung

$\displaystyle u^{\prime\prime} + \omega_0^2 u = c \cos(\omega t), \quad \omega_0>0 \,, $

beschrieben.

Die allgemeine Lösung setzt sich aus einer freien und einer erzwungenen Schwingung $ u = u_h + u_p$ zusammen, wobei

$\displaystyle u_h(t) = a \cos(\omega_0 t) + b \sin(\omega_0 t) $

und

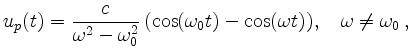
$\displaystyle u_p(t) = \frac{c}{\omega^2-\omega_0^2}\, (\cos(\omega_0 t)-\cos(\omega t)),\quad \omega \ne \omega_0 \,, $

sowie

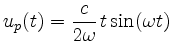
$\displaystyle u_p(t) = \frac{c}{2 \omega}\,t\sin(\omega t) $

im Resonanzfall $ \omega=\omega_0$ .

Die Konstanten $ a$ , $ b$ können durch Anfangsbedingungen festgelegt werden:

$\displaystyle a = u(0),\quad b = u^\prime(0)/\omega_0\,. $

(Inhalt vorübergehend nicht verfügbar)

(Inhalt vorübergehend nicht verfügbar)

(Inhalt vorübergehend nicht verfügbar)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 6.6.2011