Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Mehrdimensionale Integration - Kurven- und Flächenintegrale

Reguläre Parametrisierung eines Flächenstücks

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Eine stetig differenzierbare Parametrisierung

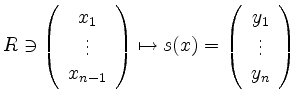
$\displaystyle R \ni\left(\begin{array}{c} x_1 \\ \vdots \\ x_{n-1} \end{array}\... ...\mapsto s(x) = \left(\begin{array}{c} y_1 \\ \vdots \\ y_n \end{array}\right) $

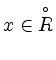über einem regulären Bereich $ R$ beschreibt ein reguläres Flächenstück $ S = s(R)$, wenn $ s$ im Inneren von $ R$ injektiv ist und die Vektoren $ \partial_1 s(x) , \ldots ,\partial_{n-1}s(x)$ für alle $ x \in\overset{\circ}{R} $ linear unabhängig sind.

\includegraphics[width=0.5\linewidth]{bild_regulaere_param}

Der bis auf das Vorzeichen eindeutig bestimmte Einheitsvektor $ \xi$, orthogonal zu der durch $ \partial_1 s(x) , \ldots ,\partial_{n-1}s(x)$ aufgespannten Tangentialebene, wird als Flächennormale bezeichnet. Er bildet zusammen mit den Vektoren $ \partial_i s(x)$ eine Basis von $ \mathbb{R}^n$.

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017