Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Mehrdimensionale Integration - Kurven- und Flächenintegrale

Flächenintegral

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Das Integral einer stetigen Funktion $ f$ über einem regulären Flächenstück $ S$ mit Parametrisierung

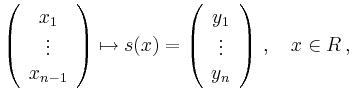
$\displaystyle \left( \begin{array}{c} x_1 \\ \vdots \\ x_{n-1} \end{array}\righ... ...\begin{array}{c} y_1 \\ \vdots \\ y_{n} \end{array}\right)\,, \quad x \in R\,, $

und Flächennormale $ \xi$ ist als

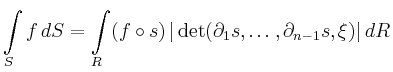
$\displaystyle \int\limits_S f \,dS= \int\limits_R (f\circ s)\,\vert\det (\partial_1 s , \ldots , \partial_{n-1} s, \xi)\vert\, dR $

definiert und unabhängig von der gewählten Parametrisierung. Der Betrag der Determinante ist der Skalierungsfaktor der Flächenelemente:

$\displaystyle dS = \vert\det (\partial_1 s , \ldots , \partial_{n-1} s, \xi)\vert\, dR \,. $

Als Spezialfall erhält man für $ f=1$ den Flächeninhalt von $ S$.

Die Glattheitsvoraussetzungen an $ f$ und $ s$ können abgeschwächt werden, indem man das Integral über einen geeigneten Grenzprozess definiert. Darüber hinaus kann eine Fläche aus mehreren Flächenstücken zusammengesetzt sein. Das Flächenintegral ist dann die Summe der Integrale über die einzelnen Flächenstücke.

(Inhalt vorübergehend nicht verfügbar)

(Inhalt vorübergehend nicht verfügbar)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017