
Mathematik-Online-Kurs: Vektoranalysis - Differentiation - Differentialoperatoren

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Kurs: Vektoranalysis - Differentiation - Differentialoperatoren | |
Rechenregeln für Differentialoperatoren erster Ordnung |
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
Bei der Hintereinanderschaltung von Gradient, Divergenz und Rotation gilt
Bei der Differentiation von Produkten gilt
Analoge Identitäten gelten auch für ebene
Felder.
Formal erhält man die entsprechenden Formeln,
wenn man die dritte Komponente der Felder null setzt
und nur von ![]() und
und ![]() abhängige Funktionen
betrachtet.
abhängige Funktionen
betrachtet.
Betrachtet man die ![]() -Komponente ergibt sich
-Komponente ergibt sich
Verwendet man die Definition der Rotation mit Hilfe des
![]() -Tensors
-Tensors
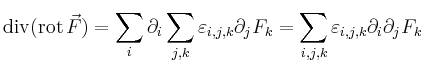
ergibt eine Vertauschung der Indizes ![]()
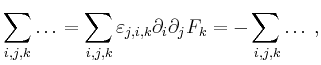
die ![]() -Komponente der linken Seite ist
-Komponente der linken Seite ist
Folgt aus der Anwendung der Produktregel auf die einzelnen Komponenten
Anwendung der Pruduktregel liefert
Mit der Definition des Kreuzproduktes und der Produktregel folgt
![$\displaystyle \operatorname{div}(\vec{F}\times \vec{G}) =
\sum_{i,j} \varepsilon_{i,j,k}\,\left(
(\partial_i F_j)G_k + [F_j(\partial_i G_k)]
\right)\,.
$](/inhalt/erlaeuterung/erlaeuterung353/img25.png)
Die Vertauschung von ![]() im zweiten Term
im zweiten Term ![]() und die Zyklizität von
und die Zyklizität von
![]() ergibt die Formel.
ergibt die Formel.
Die ![]() -Komponente von
-Komponente von
![]() ,
,
Mit Hilfe von zyklischer Vertauschung erhält man die Formel.
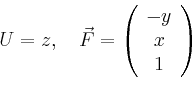
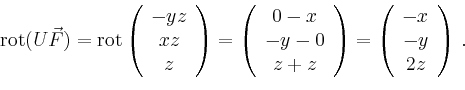
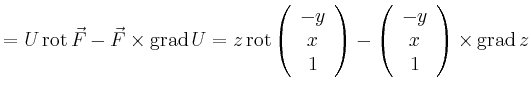 |
||
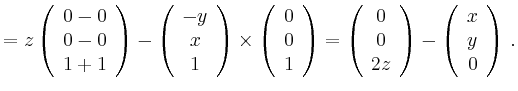 |
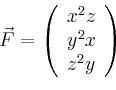
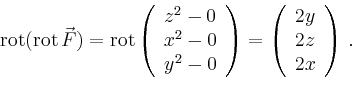
 |
||
 |
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 9.10.2013 |