
Mathematik-Online-Kurs: Vektoranalysis - Integration - Integralsätze von Gauß

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Kurs: Vektoranalysis - Integration - Integralsätze von Gauß | |
Integralsatz von Gauß |
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
Ist ![]() ein stetig differenzierbares Vektorfeld auf
einem regulären räumlichen Bereich
ein stetig differenzierbares Vektorfeld auf
einem regulären räumlichen Bereich ![]() , der durch eine Fläche
, der durch eine Fläche ![]() mit nach außen orientiertem vektoriellem Flächenelement
mit nach außen orientiertem vektoriellem Flächenelement
![]() berandet wird, so gilt
berandet wird, so gilt
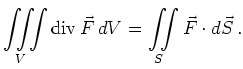
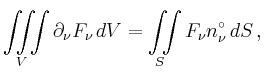
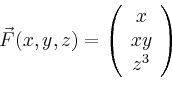
Für die Divergenz ergibt sich
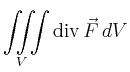 |
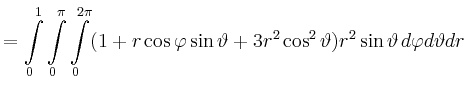 |
|
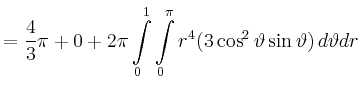 |
||
![$\displaystyle = \frac{4}{3}\pi + 2\pi\left[\frac{1}{5}r^5\right]_{r=0}^1 \left[...
...right]_{\vartheta=0}^\pi = \frac{4}{3}\pi + \frac{4}{5}\pi =\frac{32}{15}\pi\,.$](/inhalt/beispiel/beispiel720/img7.png) |
Mit der Parametrisierung
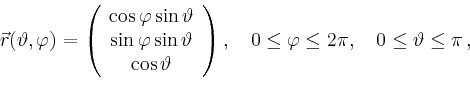
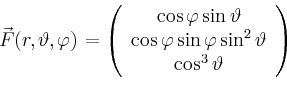
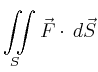 |
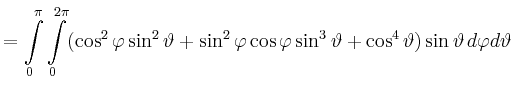 |
|
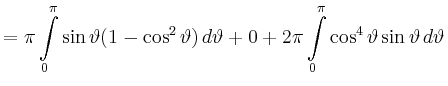 |
||
![$\displaystyle =\pi\left([-\cos\vartheta]_0^\pi +\left[\frac{1}{3}\cos^3\vartheta\right]_0^\pi\right) +2\pi\left[-\frac{1}{5}\cos^5\vartheta\right]_0^\pi$](/inhalt/beispiel/beispiel720/img15.png) |
||
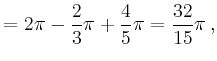 |
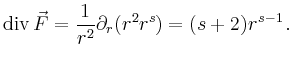
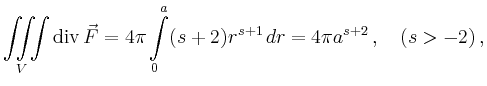
Da das Vektorfeld senkrecht auf der Kugel steht, entspricht das Flussintegral
dem Betrag des Feldes auf der Kugel, multipliziert mit dem Inhalt der
Kugeloberfläche ![]() ,
,
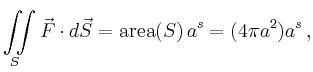
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 9.10.2013 |