Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Vektoranalysis - Integration - Integralsätze von Green und Stokes

Satz von Green

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Ist $ \vec{F}$ ein stetig differenzierbares bivariates Vektorfeld auf einem regulären ebenen Bereich $ A$ mit orientiertem Rand $ C$ , so gilt

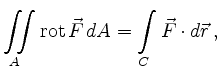
$\displaystyle \iint\limits_A \operatorname{rot} \vec{F} \, dA = \int\limits_{C} \vec{F} \cdot d\vec{r} \,, $

wobei $ \operatorname{rot} \vec{F} = \partial_x F_y -\partial_y F_x$ . Diese auf Green zurückgehende Identität ist ein Spezialfall des Satzes von Stokes.

Die Glattheitsvoraussetzungen können abgeschwächt werden, indem man die Integrale über geeignete Grenzprozesse definiert.

Der Satz ist eine unmittelbare Folgerung aus dem Hauptsatz für zweidimensionale Integrale. Dieser besagt, dass

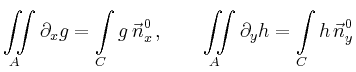
$\displaystyle \iint\limits_A \partial_x g = \int\limits_C g\,\vec{n}_x^0\,,\qquad \iint\limits_A \partial_y h = \int\limits_C h\,\vec{n}_y^0$

mit $ (\vec{n}_x^0,\vec{n}_x^0)$ der nach außen gerichteten Einheitsnormalen von $ A$. Berücksichtigt man, das

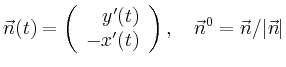
$\displaystyle \vec{n}(t)=\left(\begin{array}{r}y'(t)\\ -x'(t)\end{array}\right),\quad \vec{n}^0=\vec{n}/\vert\vec{n}\vert $

sowie die Definition des Linienelements

$\displaystyle dC=\vert\vec{n}(t)\vert\,dt$

so erhält man den Integralsatz von Green durch Substitution von $ g=F_y$ und $ h=-F_x$ in den beiden obigen Identitäten:

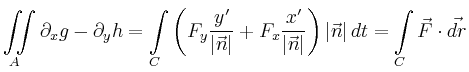
$\displaystyle \iint\limits_A \partial_x g - \partial_y h =\int\limits_C \left(... ...\vec{n}\vert}\right) \vert\vec{n}\vert\,dt =\int\limits_C \vec{F}\cdot\vec{dr} $

Wir betrachten das ebene Vektorfeld

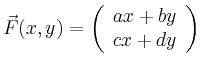
$\displaystyle \vec{F}(x,y)=\left(\begin{array}{c} ax+by\\ cx+dy\end{array}\right) $

auf der Einheitskreisscheibe

$\displaystyle K: x_1^2+x_2^2\leq 1\,. $

Für die linke Seite im Satz von Stokes erhält man

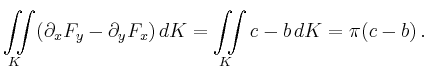
$\displaystyle \iint\limits_{K} (\partial_x F_y - \partial_y F_x)\,dK =\iint\limits_{K} c-b\,dK = \pi(c-b)\,. $

Parametrisiert man den Rand von $ K$ mit

\begin{displaymath} \vec{r}(t)=\left( \begin{array}{c} \cos t\\ \sin t\\ \end{array}\right),\quad t\in[0,2\pi]\,, \end{displaymath}

so erhält man für die rechte Seite ebenfalls

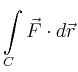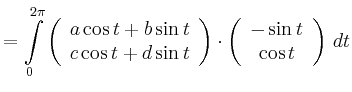$\displaystyle \int\limits_{C} \vec{F}\cdot d\vec{r}$ $\displaystyle = \int\limits_0^{2\pi} \left( \begin{array}{c} a\cos t+b\sin t\\ ... ...y}\right)\cdot\left( \begin{array}{c} -\sin t\\ \cos t\\ \end{array}\right)\,dt$    
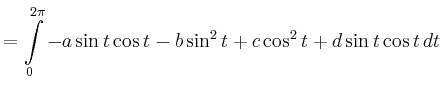  $\displaystyle =\int\limits_0^{2\pi} -a\sin t\cos t - b\sin^2 t + c\cos^2 t + d\sin t\cos t\,dt$    
  $\displaystyle = \pi(c-b)\,,$    

da

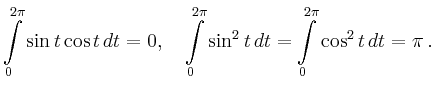
$\displaystyle \int\limits_0^{2\pi} \sin t\cos t \,dt = 0,\quad\int\limits_0^{2\pi} \sin^2 t\,dt = \int\limits_0^{2\pi} \cos^2 t\,dt =\pi\,. $

Wir betrachten das ebene Vektorfeld

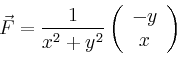
\begin{displaymath} \vec{F}=\frac{1}{x^2+y^2}\left( \begin{array}{c} -y\\ x\\ \end{array}\right) \end{displaymath}

auf der Kreisscheibe

$\displaystyle K:\quad x^2+y^2\leq r\,,\quad r>0\,. $

Obwohl die Rotation von $ \vec{F}$ verschwindet,

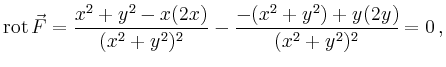
$\displaystyle \operatorname{rot}\vec{F} = \frac{x^2+y^2-x(2x)}{(x^2+y^2)^2} -\frac{-(x^2+y^2)+y(2y)}{(x^2+y^2)^2} = 0\,, $

ist das Arbeitsintegral über den Rand $ C$ von $ K$ nicht null. Verwendet man

\begin{displaymath} \vec{r}(t)=r\left( \begin{array}{c} \cos t\\ \sin t\\ \end{array}\right),\quad t\in[0,2\pi]\,, \end{displaymath}

als Parametrisierung für $ C$, so erhält man

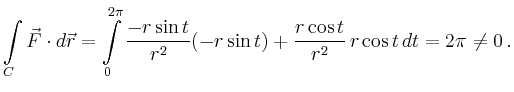
$\displaystyle \int\limits_{C} \vec{F} \cdot d\vec{r} = \int\limits_0^{2\pi} \frac{-r\sin t }{r^2}(-r\sin t )+\frac{r\cos t}{r^2}\,r\cos t\, dt = 2\pi \neq 0\,. $

Dies ist kein Widerspruch zum Satz von Green, weil das Vektorfeld $ \vec{F}$ im Inneren der Kreisscheibe bei $ (0,0)$ eine Singularität besitzt.

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 9.10.2013