Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Vektoranalysis - Differentiation - Differentialoperatoren

Divergenz

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die Divergenz eines Vektorfeldes

$\displaystyle \vec{F}(x,y,z) = F_x\vec{e}_x+F_y\vec{e}_y+F_z\vec{e}_z $

wird durch

$\displaystyle \operatorname{div} \vec{F} = \partial_x F_x + \partial_y F_y +\partial_z F_z $

definiert. Sie ist invariant unter orthogonalen Koordinatentransformationen und entspricht physikalisch der Quelldichte des Vektorfeldes.

Alternativ lässt sich die Divergenz eines stetig differenzierbaren Vektorfeldes als Grenzwert des Flusses durch die Oberfläche $ {S}$ eines den Punkt $ P$ enthaltenden räumlichen Bereichs $ {V}$ definieren:

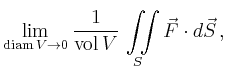
$\displaystyle \lim_{\operatorname{diam}{V}\to0} \frac{1}{\operatorname{vol}{V}}\, \iint\limits_{S} \vec{F} \cdot d\vec{S} \,, $

wobei $ d\vec{S}$ nach außen orientiert ist. Dies folgt unmittelbar aus dem Satz von Gauß und dem Mittelwertsatz und zeigt insbesondere die Invarianz der Divergenz unter orthogonalen Koordinatentransformationen.
Zur Illustration wird die Divergenz zweier typischer Felder berechnet.

Für das zentrale Kraftfeld

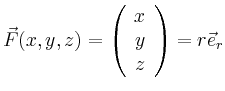
$\displaystyle \vec{F}(x,y,z) = \left(\begin{array}{c}x\\ y\\ z\end{array}\right)=r\vec{e}_r $

ist

$\displaystyle \operatorname{div}\vec{F}(x,y,z) = 1+1+1=3\,. $

Für eine wirbelförmige Strömung

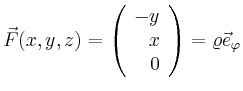
$\displaystyle \vec{F}(x,y,z) = \left(\begin{array}{r}-y\\ x\\ 0\end{array}\right)=\varrho\vec{e}_\varphi $

ist

$\displaystyle \operatorname{div}\vec{F}(x,y,z) = 0\,. $

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 9.10.2013