Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Fourier-Analysis - Fourier-Reihen - Konvergenz

Periodische quadratintegrierbare Funktionen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Der Raum der $ 2\pi$-periodischen Funktionen $ f:\ \mathbb{R}\to\mathbb{C}$ mit

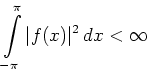
$\displaystyle \int\limits_{-\pi}^\pi \vert f(x)\vert^2\,dx < \infty $

und der durch das Skalarprodukt

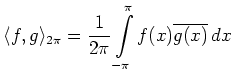
$\displaystyle \langle f,g \rangle_{2\pi} = \frac{1}{2\pi}\int\limits_{-\pi}^\pi f(x)\overline{g(x)}\,dx $

induzierten Norm $ \Vert\cdot\Vert _{2\pi}$ wird mit $ L_{2\pi}^2$ bezeichnet.

Alternativ kann der Raum der $ 2\pi$-periodischen quadratintegrierbaren Funktionen auch als Abschluss der glatten Funktionen definiert werden, d.h. jede Funktion $ f\in L_{2\pi}^2$ lässt sich durch eine Folge unendlich oft differenzierbarer Funktionen $ f_n$ approximieren:

$\displaystyle \Vert f-f_n\Vert _{2\pi} \to 0,\quad n\to \infty \,. $

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 13.11.2013