Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Fourier-Analysis - Diskrete Fourier-Transformation - Schnelle Fourier-Transformation

Schnelle Fourier-Transformation

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die diskrete Fourier-Transformation,

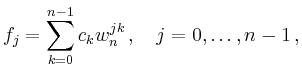
$\displaystyle f_j = \sum_{k=0}^{n-1} c_k w_n^{jk}\,, \quad j = 0,\dots,n-1\,, $

$ (w_n = \exp(2\pi \mathrm{i} / n))$, kann für $ n = 2^\ell$ mit der so genannten schnellen Fourier-Transformation (FFT, Fast Fourier Transform) mit $ 2 n \ell$-Operationen berechnet werden. In der rekursiven Version hat der Algorithmus die folgende Form:

\begin{tabbing} \qquad \= $f = \operatorname{FFT}(c)$\ \\ \> \qquad \= $n = \op... ... \> $f = (g+p\,.\!*\,h,\,g-p\,.\!*\,h)$\\ \> \> {\bf end}\\ \par \end{tabbing}

Dabei bezeichnet $ .*$ die komponentenweise Multiplikation von Vektoren, d.h. $ (a\,.\!*\,b)_j = a_jb_j$.

Die inverse diskrete Fourier-Transformation

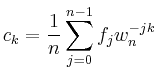
$\displaystyle c_k = \frac{1}{n} \sum_{j=0}^{n-1} f_j w_n^{-jk} $

kann vollkommen analog berechnet werden. Man bezeichnet den entsprechenden Algorithmus mit $ c = \operatorname{IFFT}(f)$.
Die induktive Herleitung des Algorithmus ist verblüffend einfach. Man spaltet die Summen

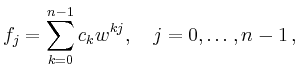
$\displaystyle f_j = \sum_{k=0}^{n-1} c_k w^{kj},\quad j=0,\ldots,n-1 \,, $

in gerade und ungerade Summanden auf:

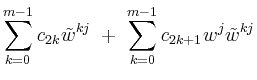
$\displaystyle \sum_{k=0}^{m-1} c_{2k} \tilde w^{kj} \ + \ \sum_{k=0}^{m-1} c_{2k+1} w^j \tilde w^{kj} $

mit $ m=n/2$ und $ \tilde w=\exp(2\pi\mathrm{i}/m)=w^2$. Bis auf den Faktor $ w^j$ entsprechen die Summen den im Algorithmus rekursiv berechneten diskreten Fourier-Transformationen der Länge $ m$:

$\displaystyle f_j = g_j + w^j h_j,\quad j=0,\ldots,m-1 \,. $

Ersetzt man in den Summen $ j$ durch $ j+m$ so ändert sich wegen $ \tilde w^m=1$ lediglich das Vorzeichen der zweiten Summe $ w^{j+m} = -w^j$. Damit folgt

$\displaystyle f_{j+m} = g_j - w^j h_j,\quad j=0,\ldots,m-1 \,, $

das heißt die Vektoren $ g$ und $ h$ lassen sich auch zur Berechnung von $ (f_m,f_{m+1},...,f_{n-1})^\mathrm{t}$ verwenden.

Die Anzahl $ \operatorname{op}(n)$ der vom FFT-Algorithmus benötigten komplexen Additionen und Multiplikationen lässt sich rekursiv bestimmen. Durch Addition der zur Berechnung von $ g$, $ h$, $ p$ und $ f$ benötigten Operationen erhält man

$\displaystyle \operatorname{op}(n) = \operatorname{op}(n/2) + \operatorname{op}(n/2) + (n/2) + 3(n/2) = 2\operatorname{op}(n/2) + 2n \,. $

Iteriert man diese Gleichung, so folgt
$\displaystyle \operatorname{op}(n)$ $\displaystyle =$ $\displaystyle 2\left(2\operatorname{op}(n/4) + 2(n/2)\right)+2n = 4\operatorname{op}(n/4) + 2n+2n$  
  $\displaystyle =$ $\displaystyle \cdots$  
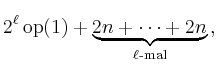  $\displaystyle =$ $\displaystyle 2^\ell\operatorname{op}(1) + \underbrace{2n + \cdots + 2n}_{\ell\text{-mal}} \,,$  

und wegen $ \operatorname{op}(1)=0$ die behauptete Gesamtoperationenzahl.
Als Beispiel wird die diskrete Fourier-Transformation des Vektors

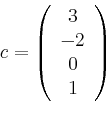
\begin{displaymath} c =\left( \begin{array}{c} 3 \\ -2 \\ 0 \\ 1\\ \end{array}\right) \end{displaymath}

berechnet.

Beim Start des Hauptprogramms wird zuerst rekursiv $ g = \operatorname{FFT}(3,0)$ und $ h = \operatorname{FFT}(-2,1)$ aufgerufen. Für die erste Rekursion ergibt sich dabei

$\displaystyle g$ $\displaystyle = 3$    
$\displaystyle h$ $\displaystyle = 0$    
$\displaystyle w_2$ $\displaystyle = \exp(2\pi\mathrm{i}/2) =-1\,,\, p=(1)$    
$\displaystyle f$ $\displaystyle = (3+1\cdot 0,3-1\cdot 0)^{\operatorname t}=(3,3)^{\operatorname t}$    

und für die zweite


$\displaystyle g$ $\displaystyle =-2$    
$\displaystyle h$ $\displaystyle =1$    
$\displaystyle w_2$ $\displaystyle = \exp(2\pi\mathrm{i}/2) =-1\,,\, p=(1)$    
$\displaystyle f$ $\displaystyle = (-2+1\cdot1,-2-1\cdot1)^{\operatorname t}=(-1,-3)^{\operatorname t}\,.$    

Zurück im Hauptprogramm erhält man damit

$\displaystyle g$ $\displaystyle = (3,3)^{\operatorname t}$    
$\displaystyle h$ $\displaystyle = (-1,-3)^{\operatorname t}$    
$\displaystyle w_4$ $\displaystyle = (\exp(2\pi\mathrm{i}/4)=\mathrm{i}\,,\,p=(1,\mathrm{i})^\mathrm{t}$    
$\displaystyle f$ $\displaystyle = (g+p.*h, g-p.*h) = (3-1\cdot 1,3-\mathrm{i}\cdot 3,3-1\cdot(-1)... ...athrm{i}\cdot (-3))^\mathrm{t} =(2,3-3\mathrm{i},4,3+3\mathrm{i})^\mathrm{t}\,.$    

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 13.11.2013