Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Fourier-Analysis - Diskrete Fourier-Transformation - Anwendungen

Trigonometrische Interpolation

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Für $ n=2^\ell$ können die Koeffzienten des trigonometrischen Polynoms

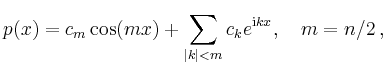
$\displaystyle p(x) = c_m \cos(mx) + \sum_{\vert k\vert<m} c_k e^{\mathrm{i}kx},\quad m=n/2 \,, $

das die Daten

$\displaystyle f_j = f(x_j),\quad x_j = 2\pi j/n,\, j=0,\ldots,n-1 \,, $

interpoliert, mit der inversen schnellen Fourier-Transformation berechnet werden:

$\displaystyle (c_0,\ldots,c_m,c_{-m+1},\ldots,c_{-1}) = \operatorname{IFFT}(f) \,. $

Die etwas ungewohnte Form des trigonometrischen Polynoms mit dem zusätzlichen Kosinus-Term ist notwendig, da die Anzahl der Daten für die Anwendung der schnellen Fourier-Transformation gerade sein muss.

Setzt man

$\displaystyle \tilde{c} = (c_0,\ldots,c_m,c_{-m+1},\ldots,c_{-1}) \,, $

so gilt mit der Fourier-Matrix $ W$

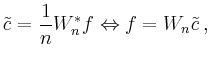
$\displaystyle \tilde{c} = \frac{1}{n} W_n^\ast f \Leftrightarrow f = W_n \tilde{c} \,, $

wobei $ \tilde{c}$ und $ f$ von 0 bis $ n-1$ indiziert werden. Letztere Identität bedeutet, dass

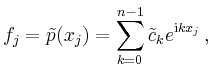
$\displaystyle f_j = \tilde p(x_j) = \sum_{k=0}^{n-1} \tilde c_k e^{\mathrm{i}kx_j} \,, $

d.h. das trigonometrische Polynom $ \tilde p$ erfüllt die Interpolationsbedingungen. Es bleibt zu zeigen, dass sich die entsprechenden Terme bei $ \tilde p$ und $ p$ ( $ \tilde c_k = c_{k-n}$, $ k=m+1,\ldots,n-1$) ersetzen lassen, ohne dass sich die Werte an den Punkten $ x_j$ verändern. Es muss also geprüft werden, ob

$\displaystyle \cos(mx_j) = \exp(\mathrm{i}mx_j),\quad \exp(\mathrm{i}kx_j) = \exp(\mathrm{i}(k-n)x_j) \,. $

Dies folgt aber unmittelbar aus

$\displaystyle mx_j = \pi j,\quad -nx_j = -2\pi j \,. $

Als Beispiel sollen die Daten

$\displaystyle f=(0.2,-6,-0.2,10,0.2,-6,-0.2,10)^{\operatorname t} $

an den Stellen

$\displaystyle x_j=2\pi j/8,\quad j=0,\ldots,7\,, $

durch ein trigonometrisches Polynom interpoliert werden.

Man erhält

$\displaystyle \tilde{c}$ $\displaystyle =\operatorname{IFFT}(f) = (1,0,0.1+4\mathrm{i},0,-1,0,0.1-4\mathrm{i},0)^{\operatorname t}$    

und damit


$\displaystyle c$ $\displaystyle = (c_{-3},\ldots,c_4)^{\operatorname t}= (0,0.1-4\mathrm{i},0,1,0,0.1+4\mathrm{i},0,-1)^{\operatorname t},$    

d.h.


$\displaystyle p(x)$ $\displaystyle = (0.1-4\mathrm{i})e^{-2\mathrm{i}x} +1 + (0.1+4\mathrm{i})e^{2\mathrm{i}x}-\cos(4x)\,.$    

Da die Daten $ f$ reell sind, ist auch $ p$ reell und die komplex konjugierten Terme lassen sich zusammenfassen:

$\displaystyle (0.1-4\mathrm{i})e^{-2\mathrm{i}x} +(0.1+4\mathrm{i})e^{2\mathrm{i}x} = 0.2 \cos(2x)-8 \sin(2x)\,. $

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 13.11.2013