Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Fourier-Analysis - Fourier-Transformation - Definition und Eigenschaften

Faltung und Fourier-Transformation

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die Faltung zweier Funktionen,

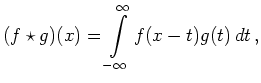
$\displaystyle (f\star g)(x) = \int\limits_{-\infty}^\infty f(x-t)g(t)\,dt\,, $

wird durch die Fourier-Transformation in ein Produkt überführt:

$\displaystyle \widehat{f\star g} = \hat{f}\hat{g} \,. $

Formal folgt die Identität unmittelbar aus der Definition. Danach ist die linke Seite

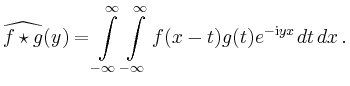
$\displaystyle \widehat{f\star g}(y) = \int\limits_{-\infty}^\infty \int\limits_{-\infty}^\infty f(x-t)g(t)e^{-\mathrm{i}yx}\,dt\,dx \,. $

Schreibt man

$\displaystyle e^{-\mathrm{i}yx} = e^{-\mathrm{i}y(x-t)} e^{-\mathrm{i}yt} $

und substituiert

$\displaystyle z = x-t,\quad dz = dx \,, $

so erhält das Integral die Produktform

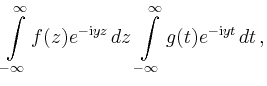
$\displaystyle \int\limits_{-\infty}^\infty f(z)e^{-\mathrm{i}yz}\,dz\, \int\limits_{-\infty}^\infty g(t)e^{-\mathrm{i}yt}\,dt \,, $

die mit der rechten Seite der zu beweisenden Identität übereinstimmt.
Als Beispiel wird die Impuls-Funktion

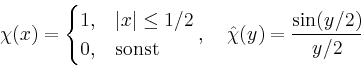
\begin{displaymath} \chi(x)= \begin{cases} 1,& \vert x\vert\leq 1/2\\ 0,& \text{sonst} \end{cases},\quad \hat{\chi}(y)=\frac{\sin(y/2)}{y/2} \end{displaymath}

betrachtet.
\includegraphics[width=.4\linewidth]{b_faltung_1}          \includegraphics[width=.4\linewidth]{b_faltung_transformiert_1}
Für die Faltung von $ \chi$ mit sich selbst erhält man

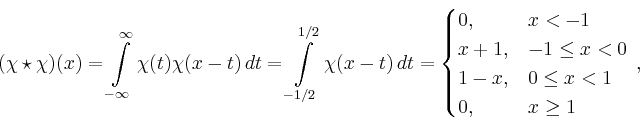
\begin{displaymath} (\chi\star \chi)(x) = \int\limits_{-\infty}^{\infty}\chi(t)\... ...1\leq x < 0\\ 1-x,& 0\leq x < 1\\ 0,& x\geq 1 \end{cases}\,, \end{displaymath}

da der Integrand $ 1$ ist, falls $ \vert x-t\vert\leq1/2$.
\includegraphics[width=.4\moimagesize]{b_faltung_2}
Als Fourier-Transformation der sogenannten Hutfunktion $ \chi\star \chi$ ergibt sich nach der Faltungsformel

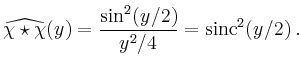
$\displaystyle \widehat{\chi\star \chi}(y)=\frac{\sin^2(y/2)}{y^2/4} =\operatorname{sinc}^2(y/2)\,. $

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 13.11.2013