Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Fourier-Analysis - Fourier-Transformation - Fundamentale Sätze

Quadratintegrierbare Funktionen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Für ein Gebiet $ D\subset\mathbb{R}^n$ bezeichnet $ L^2(D)$ den Raum der Funktionen $ f:\ D\to\mathbb{C}$ mit

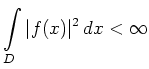
$\displaystyle \int\limits_D \vert f(x)\vert^2\,dx < \infty $

und der durch das Skalarprodukt

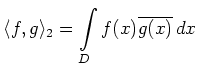
$\displaystyle \langle f,g \rangle_2 = \int\limits_D f(x)\overline{g(x)}\,dx $

induzierten Norm $ \Vert\cdot\Vert _2$.

Alternativ kann $ L^2(D)$ auch als Abschluß der glatten Funktionen definiert werden, d. h. jede quadratintegrierbare Funktion läßt sich durch eine Folge unendlich oft differenzierbarer Funktionen $ f_n$ approximieren:

$\displaystyle \Vert f-f_n\Vert \to 0,\quad n\to \infty \,. $

Als Beispiel wird die Funktion

$\displaystyle f(x)=\vert x\vert^s $

auf der $ n$-dimensionalen Einheitskugel

$\displaystyle D=\{x\in\mathbb{R}^n:\vert x\vert < 1\} $

betrachtet.

Mit Kugelkoordinaten ($ r=\vert x\vert$) erhält man

$\displaystyle \int\limits_D \vert f(x)\vert^2\,dx = c\,\int\limits_0^1 r^{2s} r^{n-1}\,dr = c\, \left[\frac{r^{2s+n}}{2s+n}\right]_0^1\,, $

d.h. $ f$ ist quadratintegrierbar für $ 2s> -n$.

Betrachtet man dieselbe Funktion auf dem Gebiet

$\displaystyle \tilde{D}=\{x\in\mathbb{R}^n : \vert x\vert >1 \}\,, $

so erhält man wiederum mit Kugelkoordinaten

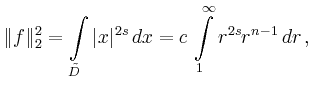
$\displaystyle \Vert f\Vert _2^2 = \int\limits_{\tilde{D}} \vert x\vert^{2s} \,dx= c\,\int\limits_1^\infty r^{2s}r^{n-1}\,dr\,, $

d.h. $ f$ ist quadratintegrierbar für $ 2s<-n$.
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 13.11.2013