Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Fourier-Analysis - Fourier-Transformation - Fundamentale Sätze

Satz von Plancherel

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Bis auf einen Normierungsfaktor lässt die Fourier-Transformation das Skalarprodukt und damit auch die Norm auf $ L^2(\mathbb{R})$ invariant:

$\displaystyle 2\pi\langle f,g\rangle = \langle \hat{f}, \hat{g} \rangle,\quad \sqrt{2\pi}\Vert f\Vert = \Vert\hat{f}\Vert \,. $

Aufgrund dieser Eigenschaft lässt sich die Fourier-Transformation auf $ L^2(\mathbb{R})$ durch einen Grenzprozess definieren. Für eine quadratintegrierbare Funktion $ f$ wählt man eine approximierende Folge glatter Funktionen $ f_n$ mit kompaktem Träger ( $ \Vert f-f_n\Vert\to 0$) und definiert

$\displaystyle \hat{f} = \lim_{n\to\infty} \hat{f}_n \,. $

Formal lässt sich die Identität für das Skalarprodukt herleiten, indem man $ f$ als die inverse Fourier-Transformation einer Funktion $ h$ wählt. Dann ist die linke Seite gleich

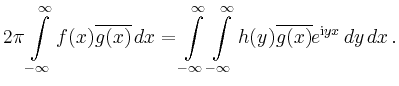
$\displaystyle 2\pi \int\limits_{-\infty}^\infty f(x)\overline{g(x)}\,dx = \int\... ...y \int\limits_{-\infty}^\infty h(y)\overline{g(x)}e^{\mathrm{i}yx}\,dy\,dx \,. $

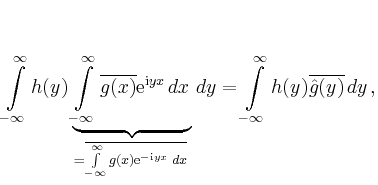
Integriert man zuerst über $ x$, so erhält man

$\displaystyle \int\limits_{-\infty}^\infty h(y) \underbrace{\int\limits_{-\inft... ...x}\,dx}}\,dy = \int\limits_{-\infty}^\infty h(y) \overline{\hat{g}(y)}\,dy \,, $

also $ \langle h,\hat{g}\rangle$, wie behauptet.
Als Beispiel wird die Funktion

$\displaystyle f(x)=e^{-x^2/2},\quad\hat{f}(y)=\sqrt{2\pi}e^{-y^2/2} $

betrachtet.

Man erhält

$\displaystyle \Vert\hat{f}\Vert^2=\langle\hat{f},\hat{f}\rangle=\langle \sqrt{2\pi}f,\sqrt{2\pi}f \rangle = 2\pi\Vert f\Vert^2 $

im Einklang mit dem Satz. Der konkrete Wert der Norm ist

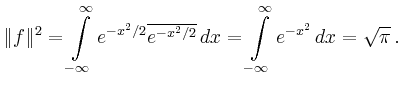
$\displaystyle \Vert f\Vert^2 = \int\limits_{-\infty}^\infty e^{-x^2/2}\overline{e^{-x^2/2}}\,dx =\int\limits_{-\infty}^\infty e^{-x^2}\,dx =\sqrt{\pi}\,. $

Als Beispiel wird die Funktion

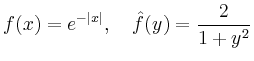
$\displaystyle f(x)=e^{-\vert x\vert},\quad\hat{f}(y)=\frac{2}{1+y^2} $

betrachtet.

Man erhält mit Hilfe einer Partialbruchzerlegung

$\displaystyle \Vert f\Vert^2$ $\displaystyle =2 \int\limits_0^\infty e^{-2x}\,dx =\left[-e^{-2x}\right]_0^\infty=1$    

und


$\displaystyle \Vert\hat{f}\Vert^2$ $\displaystyle = \int\limits_{-\infty}^\infty \frac{4}{(1+y^2)^2}\,dy = \left[ \frac{2y}{1+y^2}+2\arctan(y)\right]_{-\infty}^\infty=2\pi\,.$    

Für das Integral
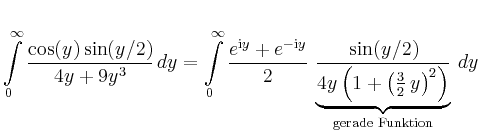$\displaystyle I$ $\displaystyle =$ $\displaystyle \int\limits_0^\infty\frac{\cos(y)\sin(y/2)}{4y+9y^3}\,dy = \int\l... ...4y\left(1+\left(\frac{3}{2}\,y\right)^2\right)}}_{\textrm{gerade Funktion}}\,dy$  
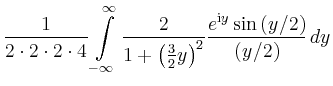  $\displaystyle =$ $\displaystyle \frac{1}{2\cdot 2\cdot 2\cdot 4}\int\limits_{-\infty}^\infty \frac{2}{1+\left(\frac{3}{2}y\right)^2} \frac{e^{\mathrm{i}y}\sin{(y/2)}}{(y/2)} \,dy$  

ergibt sich mit

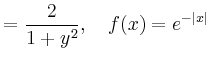$\displaystyle \hat{f}(y)$ $\displaystyle =\frac{2}{1+y^2},\quad f(x)=e^{-\vert x\vert}$    
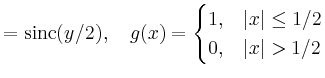$\displaystyle \hat{g}(y)$ $\displaystyle =\operatorname{sinc}(y/2),\quad g(x)= \begin{cases}1, & \vert x\vert\le 1/2\\ 0, & \vert x\vert>1/2 \end{cases}$    

der Skalierungsformel und dem Satz von Plancherel
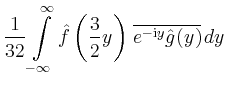$\displaystyle I$ $\displaystyle =$ $\displaystyle \frac{1}{32} \int\limits_{-\infty}^\infty \hat{f}\left(\frac{3}{2}y\right)\,\overline{e^{-\mathrm{i}y}\hat{g}(y)}\,dy$  
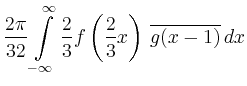  $\displaystyle =$ $\displaystyle \frac{2\pi}{32}\int\limits_{-\infty}^\infty \frac{2}{3}f\left(\frac{2}{3}x\right) \,\overline{g(x - 1)}\,dx$  
  $\displaystyle =$ $\displaystyle \frac{\pi}{24}\int\limits_{1/2}^{3/2}e^{-\frac{2}{3}\vert x\vert}... ...t]_{1/2}^{3/2} =\frac{\pi}{16}\left(\frac{1}{\sqrt[3]{e}}-\frac{1}{e}\right)\,.$  

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 13.11.2013