Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Fourier-Analysis - Fourier-Reihen - Kosinus- und Sinusreihen

Skalierung des Periodizitätsintervalls bei reellen Fourier-Reihen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die Fourier-Reihe einer $ h$-periodischen Funktion $ f$ erhält man durch lineare Transformation auf das Intervall $ [-\pi,\pi]$. Alternativ lassen sich die Fourier-Koeffizienten auch direkt berechnen:

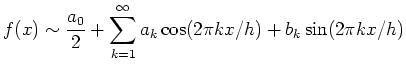
$\displaystyle f(x) \sim \frac{a_0}{2} + \sum_{k=1}^\infty a_k \cos(2\pi kx/h) + b_k \sin(2\pi kx/h) $

mit

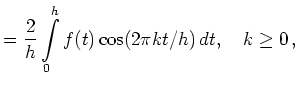$\displaystyle a_k$ $\displaystyle = \frac{2}{h} \int\limits_0^h f(t)\cos(2\pi kt/h)\,dt,\quad k\ge0\,,$    
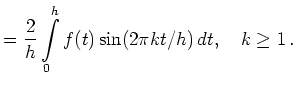$\displaystyle b_k$ $\displaystyle = \frac{2}{h} \int\limits_0^h f(t)\sin(2\pi kt/h)\,dt,\quad k\ge1\,.$    

Es wird die Fourier-Reihe der $ h$-periodischen Fortsetzung der Funktion

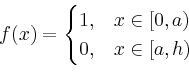
\begin{displaymath} f(x)= \begin{cases} 1, & x\in[0,a)\\ 0, & x\in[a,h)\\ \end{cases}\end{displaymath}

mit $ 0<a<h$ gesucht.

Man erhält

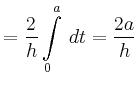$\displaystyle a_0$ $\displaystyle = \frac{2}{h} \int\limits_0^a \,dt = \frac{2a}{h}$    

und für $ k\ge1$


$\displaystyle a_k$ $\displaystyle = \frac{2}{h} \int\limits_0^a \cos(2\pi kt/h)\,dt = \frac{2}{h}\left[\frac{h\sin(2\pi kt/h)}{2\pi k}\right]_0^a = \frac{\sin(2\pi ka/h)}{\pi k}\,,$    
$\displaystyle b_k$ $\displaystyle = \frac{2}{h} \int\limits_0^a \sin(2\pi kt/h)\,dt = \frac{2}{h}\left[-\frac{h\cos(2\pi kt/h)}{2\pi k}\right]_0^a =\frac{1-\cos(2\pi ka/h)}{\pi k}$    

und somit die Fourier-Reihe

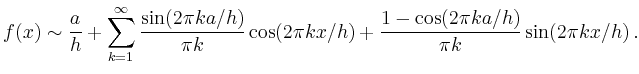
$\displaystyle f(x)\sim \frac{a}{h}+\sum_{k=1}^\infty \frac{\sin(2\pi ka/h)}{\pi k}\cos(2\pi kx/h) + \frac{1-\cos(2\pi ka/h)}{\pi k}\sin(2\pi kx/h)\,. $

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 13.11.2013