Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Repetitorium HM III - Funktionentheorie

Differentiation komplexer Funktionen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Sei $ \mbox{$f(z) = u(x,y) + \mathrm{i}v(x,y)$}$ eine komplexwertige Funktion, $ \mbox{$u$}$ und $ \mbox{$v$}$ reellwertig, $ \mbox{$z = x + \mathrm{i}y$}$, $ \mbox{$x$}$, $ \mbox{$y$}$ reell. Sei $ \mbox{$f$}$ in $ \mbox{$z_0$}$ differenzierbar, d.h. existiere der Grenzwert $ \mbox{$\lim_{z\to z_0} \frac{f(z) - f(z_0)}{z-z_0}$}$.

Insbesondere stimmt

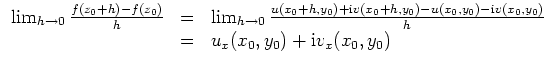
$ \mbox{$\displaystyle \begin{array}{rcl} \lim_{h\to 0} \frac{f(z_0 + h) - f(z_... ..._0,y_0)}{h} \\ & = & u_x(x_0,y_0) + \mathrm{i}v_x(x_0,y_0) \\ \end{array}$}$
mit
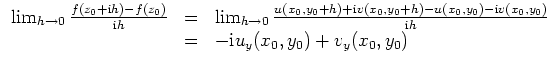
$ \mbox{$\displaystyle \begin{array}{rcl} \lim_{h\to 0} \frac{f(z_0 + \mathrm{i... ...athrm{i}h} \\ & = & -\mathrm{i}u_y(x_0,y_0) + v_y(x_0,y_0) \\ \end{array}$}$
überein, wobei $ \mbox{$h$}$ eine reelle Variable bezeichne und $ \mbox{$z_0 = x_0 + \mathrm{i}y_0$}$ geschrieben wird mit $ \mbox{$x_0$}$ und $ \mbox{$y_0$}$ reell. Abgleich von Real- und Imaginärteil liefert die Cauchy-Riemannschen Differentialgleichungen
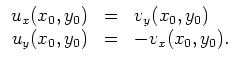
$ \mbox{$\displaystyle \begin{array}{rcl} u_x(x_0,y_0) & = & v_y(x_0,y_0) \\ u_y(x_0,y_0) & = & -v_x(x_0,y_0). \\ \end{array}$}$
Ist $ \mbox{$f$}$ in jedem Punkt eines Gebiets $ \mbox{$G\subseteq \mathbb{C}$}$ differenzierbar, so sagt man auch, $ \mbox{$f$}$ ist holomorph auf $ \mbox{$G$}$. Ein Gebiet bezeichnet hierbei eine offene, zusammenhängende Teilmenge von $ \mbox{$\mathbb{C}$}$.
(Autoren: Künzer/Meister/Nebe)

Beispiele

Aufgaben

  automatisch erstellt am 21.3.2003