
Mathematik-Online-Kurs: Repetitorium HM III - Funktionentheorie

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Kurs: Repetitorium HM III - Funktionentheorie | |
Differentiationsregeln |
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
Diese gelten wie im Reellen. Seien
![]() holomorphe Funktionen auf dem
Gebiet
holomorphe Funktionen auf dem
Gebiet
![]() , seien
, seien
![]() . Die Differentiation ist linear,
und es gelten Produkt- und Quotientenregel wie folgt.
. Die Differentiation ist linear,
und es gelten Produkt- und Quotientenregel wie folgt.
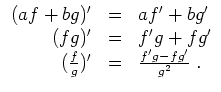
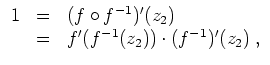
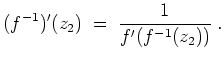
| automatisch erstellt am 21.3.2003 |