Mathematik-Online-Kurs: Formelsammlung-Vektoranalysis-Integration

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Kurs: Formelsammlung - Vektoranalysis
	Integration

[vorangehende Seite] [nachfolgende Seite]

[Gesamtverzeichnis][Seitenübersicht]

	Parametrisierung	Kurve $C:\ [a,b]\ni t\mapsto \vec{r}\,(t)$ Fläche $S:\ D\ni (u,v)\mapsto \vec{r}\,(u,v)$

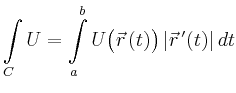	Kurvenintegral	$\displaystyle\int\limits_C U = \displaystyle\int\limits_a^b U\big(\vec{r}\,(t)\big)\,\vert\vec{r}\,'(t)\vert\,dt$

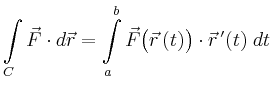	Arbeitsintegral	$\displaystyle\int\limits_C \vec{F} \cdot d\vec{r} = \displaystyle\int\limits_a^b \vec{F}\big(\vec{r}\,(t)\big) \cdot \vec{r}\,'(t) \;dt$

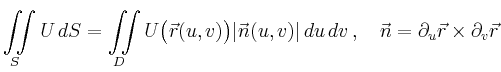	Flächenintegral	$\displaystyle\iint\limits_S U \,dS = \displaystyle\iint\limits_D U\big(\vec... ...ert \,du\,dv \,, \quad \vec{n} = \partial_u \vec{r} \times \partial_v \vec{r}$

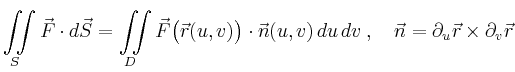	Flussintegral	$\displaystyle\iint\limits_S \vec{F} \cdot d\vec{S} = \displaystyle\iint\lim... ...) \,du\,dv \,, \quad \vec{n} = \partial_u \vec{r} \times \partial_v \vec{r}$

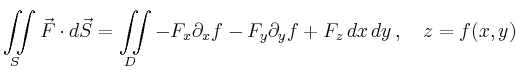	Fluss durch Funktionsgraph	$\displaystyle\iint\limits_S \vec{F} \cdot d\vec{S} = \displaystyle\iint\limits_D -F_x\partial_x f - F_y \partial_y f + F_z \,dx\,dy \,, \quad z = f(x,y)$

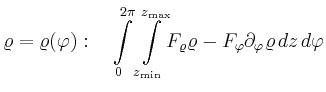
	Fluss durch Zylindermantel	$\varrho = \varrho(\varphi) : \quad \displaystyle\int\limits_{0}^{2\pi} {\d... ...}}} F_\varrho \varrho - F_\varphi \partial_\varphi \varrho \,dz\, d\varphi$ $\varrho = \varrho(z) : \quad \displaystyle\int\limits_0^{2\pi}\displaystyle\... ...z_{\max}} F_\varrho \varrho - F_z \varrho \partial_z \varrho \,dz\,d\varphi$ speziell $2\pi a (z_{\max}-z_{\min}) f(a)$ für $\vec{F} = f(\varrho)\vec{e}_\varrho$ mit $\varrho = a$

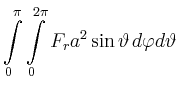	Fluss durch Kugeloberfläche	$\displaystyle\int\limits_0^\pi\displaystyle\int\limits_0^{2\pi} F_r a^2 \sin\vartheta\, d\varphi d\vartheta$ mit speziell $4\pi a^2 f(a)$ für $\vec{F} = f(r)\vec{e}_r$

vektorielle
Kurvenintegrale
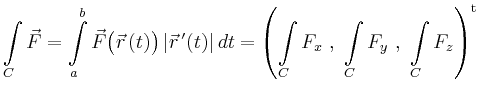$\displaystyle \int\limits_C \vec{F} = \int\limits_a^b \vec{F}\big(\vec{r}\,... ... F_x\ , \ \int\limits_C F_y\ , \ \int\limits_C F_z \right)^{\operatorname t}$

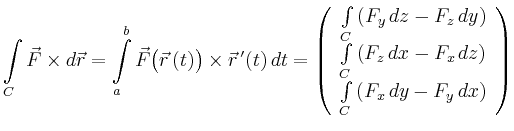$\displaystyle \int\limits_C \vec{F}\times d\vec{r} = \int\limits_a^b \vec{F}... ...z\right)\\ \int\limits_C \left(F_x\,dy-F_y\,dx\right) \end{array} \right)$

vektorielle
Flächenintegrale
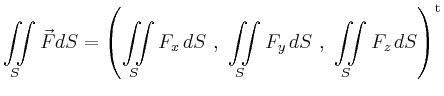
$\displaystyle \iint\limits_S \vec{F} dS = \left( \iint\limits_S F_x\, dS\ ,... ...iint\limits_S F_y\, dS\ , \ \iint\limits_S F_z\, dS \right)^{\operatorname t}$
$\displaystyle\iint\limits_S U d\vec{S} = \iint\limits_S U(\vec{r}\,)\, \vec{n}^{\,\circ}\, dS$
$\displaystyle\iint\limits_S \vec{F} \times d\vec{S} = \iint\limits_S \vec{F}(\vec{r}\,) \times \vec{n}^{\,\circ}\,dS$

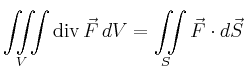
Satz von Gauß $\displaystyle\iiint\limits_V \operatorname{div} \vec{F} \, dV = \displaystyle\iint\limits_S \vec{F} \cdot d\vec{S}$
$\displaystyle\iiint\limits_V \operatorname{grad} U \, dV = \displaystyle\iint\limits_S U \, d\vec{S}$
$\displaystyle\iiint\limits_V \operatorname{rot} \vec{F} \, dV = - \displaystyle\iint\limits_S \vec{F} \times d\vec{S}$
$\displaystyle\iint\limits_A \operatorname{div} \vec{F} \, dA = \displaystyle\int\limits_C \vec{F} \times d\vec{r}\,,\quad A\subset \mathbb{R}^2$

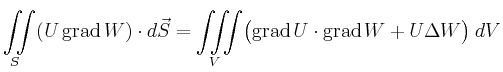
Greensche Integralformeln $\displaystyle\iint\limits_S (U \operatorname{grad} W) \cdot d\vec{S} = \disp... ... \operatorname{grad} U \cdot \operatorname{grad} W + U \Delta W \bigr)\,dV$
$\displaystyle\iint\limits_S \bigl( U \operatorname{grad} W - W \operatorname... ...cdot d\vec{S} = \displaystyle\iiint\limits_V (U\Delta W - W \Delta U ) \, dV$

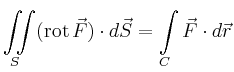
Satz von Stokes $\displaystyle\iint\limits_S (\operatorname{rot} \vec{F}) \cdot d\vec{S} = \displaystyle\int\limits_C \vec{F}\cdot d\vec{r}$
$-\displaystyle\iint\limits_S (\operatorname{grad} U) \times d\vec{S} = \displaystyle\int\limits_C U\, d\vec{r}$
$\displaystyle\iint\limits_A \operatorname{rot} \vec{F} \,dA = \displaystyle\int\limits_C \vec{F}\cdot \,d\vec{r}\,,\quad A\subset \mathbb{R}^2$

Skalares Potential Skalarfeld mit $\operatorname{grad} U = \vec{F}$
notwendige Bedingung für Existenz: $\operatorname{rot} \vec{F} = \vec 0$ , hinreichend auf einfach zusammenhängenden Gebieten

ein beliebiger, in von nach verlaufender Weg:
$\displaystyle\int\limits_C \vec{F} \cdot d\vec{r} = U(B) - U(A)\ \Rightarrow$ Wegunabhängigkeit des Integrals

Vektorpotential Vektorfeld $\vec{A}$ mit $\operatorname{rot}\vec{A} = \vec{F}$
notwendige Bedingung für Existenz: $\operatorname{div}\vec{F}=0$ , hinreichend auf einfach zusammenhängenden Gebieten

(Autoren: Reble/Wipper)

[vorangehende Seite] [nachfolgende Seite]

[Gesamtverzeichnis][Seitenübersicht]

automatisch erstellt am 31.1.2006

	vektorielle Kurvenintegrale	$\displaystyle \int\limits_C \vec{F} = \int\limits_a^b \vec{F}\big(\vec{r}\,... ... F_x\ , \ \int\limits_C F_y\ , \ \int\limits_C F_z \right)^{\operatorname t}$
		$\displaystyle \int\limits_C \vec{F}\times d\vec{r} = \int\limits_a^b \vec{F}... ...z\right)\\ \int\limits_C \left(F_x\,dy-F_y\,dx\right) \end{array} \right)$

	vektorielle Flächenintegrale	$\displaystyle \iint\limits_S \vec{F} dS = \left( \iint\limits_S F_x\, dS\ ,... ...iint\limits_S F_y\, dS\ , \ \iint\limits_S F_z\, dS \right)^{\operatorname t}$ $\displaystyle\iint\limits_S U d\vec{S} = \iint\limits_S U(\vec{r}\,)\, \vec{n}^{\,\circ}\, dS$ $\displaystyle\iint\limits_S \vec{F} \times d\vec{S} = \iint\limits_S \vec{F}(\vec{r}\,) \times \vec{n}^{\,\circ}\,dS$

	Satz von Gauß	$\displaystyle\iiint\limits_V \operatorname{div} \vec{F} \, dV = \displaystyle\iint\limits_S \vec{F} \cdot d\vec{S}$ $\displaystyle\iiint\limits_V \operatorname{grad} U \, dV = \displaystyle\iint\limits_S U \, d\vec{S}$ $\displaystyle\iiint\limits_V \operatorname{rot} \vec{F} \, dV = - \displaystyle\iint\limits_S \vec{F} \times d\vec{S}$ $\displaystyle\iint\limits_A \operatorname{div} \vec{F} \, dA = \displaystyle\int\limits_C \vec{F} \times d\vec{r}\,,\quad A\subset \mathbb{R}^2$

	Greensche Integralformeln	$\displaystyle\iint\limits_S (U \operatorname{grad} W) \cdot d\vec{S} = \disp... ... \operatorname{grad} U \cdot \operatorname{grad} W + U \Delta W \bigr)\,dV$ $\displaystyle\iint\limits_S \bigl( U \operatorname{grad} W - W \operatorname... ...cdot d\vec{S} = \displaystyle\iiint\limits_V (U\Delta W - W \Delta U ) \, dV$

	Satz von Stokes	$\displaystyle\iint\limits_S (\operatorname{rot} \vec{F}) \cdot d\vec{S} = \displaystyle\int\limits_C \vec{F}\cdot d\vec{r}$ $-\displaystyle\iint\limits_S (\operatorname{grad} U) \times d\vec{S} = \displaystyle\int\limits_C U\, d\vec{r}$ $\displaystyle\iint\limits_A \operatorname{rot} \vec{F} \,dA = \displaystyle\int\limits_C \vec{F}\cdot \,d\vec{r}\,,\quad A\subset \mathbb{R}^2$

	Skalares Potential	Skalarfeld mit $\operatorname{grad} U = \vec{F}$ notwendige Bedingung für Existenz: $\operatorname{rot} \vec{F} = \vec 0$ , hinreichend auf einfach zusammenhängenden Gebieten
		ein beliebiger, in von nach verlaufender Weg: $\displaystyle\int\limits_C \vec{F} \cdot d\vec{r} = U(B) - U(A)\ \Rightarrow$ Wegunabhängigkeit des Integrals

	Vektorpotential	Vektorfeld $\vec{A}$ mit $\operatorname{rot}\vec{A} = \vec{F}$ notwendige Bedingung für Existenz: $\operatorname{div}\vec{F}=0$ , hinreichend auf einfach zusammenhängenden Gebieten