Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Partielle Differentialgleichungen - Poisson-Gleichung

Poisson-Formel für eine Kreisscheibe

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Eine auf einer Kreisscheibe

$\displaystyle B:\ r = \vert(x,y)\vert < R $

harmonische und auf $ \bar B$ stetige Funktion $ u$ lässt sich in Polarkoordinaten in eine Fourier-Reihe

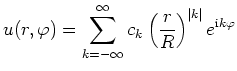
$\displaystyle u(r,\varphi) = \sum_{k=-\infty}^\infty c_k \left(\frac{r}{R}\right)^{\vert k\vert} e^{\mathrm{i}k\varphi} $

entwickeln. Die Koeffizienten erhält man aus den Randwerten:

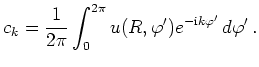
$\displaystyle c_k = \frac{1}{2\pi}\int_0^{2\pi} u(R,\varphi^\prime)e^{-\mathrm{i}k\varphi^\prime}\,d\varphi^\prime \,. $

Somit ergibt sich in Polarkoordinaten die Integraldarstellung

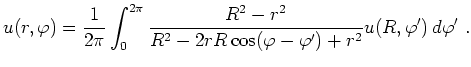
$\displaystyle u(r,\varphi)=\frac{1}{2\pi}\int_0^{2\pi}\frac{R^2-r^2} {R^2-2rR\cos(\varphi-\varphi')+r^2}u(R,\varphi')\,d\varphi'\ . $

Als Spezialfall erhält man für $ r=0$ die sogenannte Mittelwerteigenschaft harmonischer Funktionen:

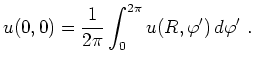
$\displaystyle u(0,0)=\frac{1}{2\pi}\int_0^{2\pi}u(R,\varphi')\,d\varphi'\ . $

Aus der Poisson-Formel folgt, dass harmonische Funktionen im Inneren ihres Definitionsgebietes unendlich oft differenzierbar sind. Desweiteren gilt das Maximumprinzip:

$\displaystyle \vert u(r,\varphi)\vert \le \max_{\varphi^\prime} \vert u(R,\varphi^\prime)\vert \,. $

(Inhalt vorübergehend nicht verfügbar)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.5.2011