Mathematik-Online-Kurs: Partielle Differentialgleichungen-Wellengleichung-Cauchy-Problem für die dreidimensionale Wellengleichung

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Kurs: Partielle Differentialgleichungen - Wellengleichung
	Cauchy-Problem für die dreidimensionale Wellengleichung

Die Lösung des Anfangswertproblems

$\displaystyle u_{tt}$	$\displaystyle =$	$\displaystyle c^2 \Delta_x u\ ,\quad x\in\mathbb{R}^3\ ,\ t\geq 0\ ,$
$\displaystyle u(x,0)$	$\displaystyle =$	$\displaystyle a(x)$
$\displaystyle u_t(x,0)$	$\displaystyle =$	$\displaystyle b(x)$

lässt sich in der Form

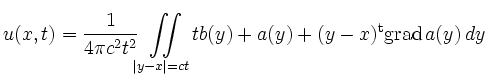
$\displaystyle u(x,t)=\frac{1}{4\pi c^2t^2}\iint\limits_{\vert y-x\vert=ct}tb(y)+a(y)+ (y-x)^{\operatorname t}{\operatorname{grad}\,} a(y)\,dy$

darstellen.

$\includegraphics[width=0.5\moimagesize]{wellengl.eps}$

Insbesondere hängt also nur von Werten entlang des abgebildeten Lichtkegels ab.

(Inhalt vorübergehend nicht verfügbar)

Für radial symmetrische Anfangswerte

$\displaystyle u(x,0)=\varphi(r)\,,\,u_t(x,0)=\psi(r)\,,\quad r=\vert x\vert\,,$

gilt für die Lösung der Wellengleichung im Ursprung

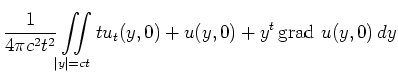$\displaystyle u(0,0,0,t)$	$\displaystyle =$	$\displaystyle \frac{1}{4\pi c^2t^2}\iint\limits_{\vert y\vert=ct}tu_t(y,0)+u(y,0)+y^t\operatorname{grad}\,u(y,0)\,dy$
	$\displaystyle =$	$\displaystyle t\psi(ct)+\varphi(ct)+ct\varphi^\prime(ct)\,.$

Fallen $\psi$ oder $\varphi^\prime$ schwächer als

ab, so strebt

gegen unendlich. Dieser Effekt wird als Fokussierung bezeichnet. Singularitäten werden durch die Wellengleichung gebündelt.

(Autor: Kimmerle)

automatisch erstellt am 5.5.2011