Reelle Spiegelungsgruppen

Zunächst werden Resultate über reelle Spiegelungsgruppen vorgestellt.

Definition 1.1 (Hyperebenenspiegelungen, reelle Spiegelungsgruppen)

Sei V ein reeller endlich-dimensionaler Vektorraum.

(i) Eine Hyperebenspiegelung ist ein nichttriviales Element $\rho$ $\in$ GL(V) endlicher Ordnung, das eine Hyperebene punktweise fest läßt.

(ii) Als endliche (reelle) Spiegelungsgruppe wird eine endliche, von Hyperebenenspiegelungen erzeugte Untergruppe der GL(V) bezeichnet.

Bemerkung 1.2 Jede Hyperebenenspiegelung $\rho$ hat die Jordansche Normalform

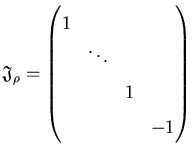
$\displaystyle \mathfrak{J}_{\rho}=\begin{pmatrix}1 &&&\\ & \ddots &&\\ &&1& \\ &&&-1 \end{pmatrix}$

Weil $\rho$ eine Hyperebene fixiert, müssen alle Einträge bis auf einen gleich 1 sein und weil $\rho$ endliche Ordnung haben soll, muß der letzte Eintrag dann eine Einheitswurzel enthalten. Die einzige nichttriviale relle Einheitswurzel ist aber -1.

Reelle Spiegelungsgruppen haben eine weitere interessante Eigenschaft: sie sind Coxetergruppen, das heißt sie besitzen eine Präsentation der Form

G = $\displaystyle \langle$ t₁,, t_n | t₁² = t_n² = 1,(t_it_j)^m_ij = 1, wobei m_ij $\displaystyle \in$ $\displaystyle \mathbb {N}$ , m_ij $\displaystyle \geq$ 2 für i $\displaystyle \not=$ j $\displaystyle \rangle$ .

Diese spezielle Präsentation mit Erzeugenden und Relationen kann man sich nun durch Graphen schön veranschaulichen: Erzeugende s_i werden durch Knoten repräsentiert, die Relationen durch Verbindungskanten zwischen den Knoten s_i und s_j. Die genaue Schreibweise wird später, bei den verallgemeinerten Graphen für komplexe Spiegelungsgruppen, noch genauer erläutert.

Hier nur ein Beispiel: Die Diedergruppe D₅ der Ordnung 10 besitzt die Präsentation

Der zugehörige Graph sieht so aus:

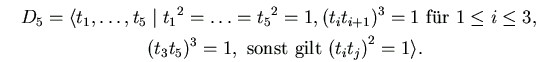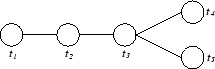
$\epsfig{file=../Diagramme/D5.eps}$

Die zu den Coxetergruppen korrespondierenden Graphen werden als Coxetergraphen bezeichnet.

Alle reellen Spiegelungsgruppen sind also Coxetergruppen. Umgekehrt gilt, daß alle endlichen Coxetergruppen als reelle Spiegelungsgruppen dargestellt werden können, d. h. die endlichen reellen Spiegelungsgruppen sind genau die endlichen Coxetergruppen.

Jahn, Heinz, Todorovic 2002-02-28