Komplexe Spiegelungsgruppen

Im Prinzip sind komplexe Spiegelungsgruppen eine Übertragung der reellen Spiegelungsgruppen in einen komplexen Vektorraum. Deshalb definiert man ganz analog:

Definition 1.3 (Pseudoreflexionen, komplexe Spiegelungsgruppen)

Sei V ein komplexer endlich-dimensionaler Vektorraum.

(i) Eine Pseudoreflexion $\rho$ ist ein nichttriviales Element endlicher Ordnung der GL(V), das eine Hyperebene punktweise fest läßt.

(ii) Eine komplexe Spiegelungsgruppe ist eine endliche, von Pseudoreflexionen erzeugte Untergruppe der GL(V). N^*(G) bezeichne dabei die Anzahl der Pseudoreflexionen in G.

Bemerkung 1.4 Ganz analog zu den reellen Hyperebenenspiegelungen hat eine Pseudoreflexion $\rho$ die Jordansche Normalform

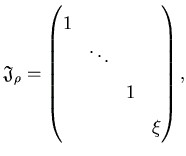
$\displaystyle \mathfrak{J}_{\rho}=\begin{pmatrix}1 &&&\\ & \ddots &&\\ &&1& \\ &&&\xi \end{pmatrix},$

$\xi$ $\not1$ ist hierbei eine o( $\rho$ )-te Einheitswurzel.

Hier läßt sich nun ein Zusammenhang zur gewöhnlichen Darstellungstheorie herstellen:

Die Einbettung einer endlichen Untergruppe G in GL(V) kann auch als eine Darstellung von G im darstellungstheoretischen Sinne betrachtet werden. Als Spiegelungsdarstellung soll eine treue Darstellung $\rho$ von G, derart daß $\rho$ (G) eine komplexe Spiegelungsgruppe ist, bezeichnet werden.

Definition 1.5 (irreduzibel, Dimension)

(i) Eine Spiegelungsgruppe G heißt irreduzibel, wenn ihre zugehörige Spiegelungsdarstellung irreduzibel ist, d. h. wenn sie keinen echten Unterraum der V invariant läßt. Ansonsten heißt sie reduzibel.

(ii) Die Dimension einer Spiegelungsgruppe bezeichne den Grad der Spiegelungsdarstellung.

A priori ist nicht klar, daß die Dimension eindeutig ist. Ein und diesselbe Gruppe könnte ja zwei Spiegelungsdarstellungen von unterschiedlichem Grad haben. Vermutlich ist das nicht möglich, in der Literatur war leider nichts genaueres dazu zu finden. Die Eindeutigkeit des Dimension wird im folgenden aber auch nicht benötigt.

Ist eine Spiegelungsgruppe reduzibel, zerfällt sie in ein direktes Produkt von Spiegelungsgruppen kleinerer Dimension. Dies gilt, weil nach dem Satz von Maschke der komplexe Gruppenring $\mathbb {C}$ G halbeinfach ist und damit reduzible $\mathbb {C}$ G-Moduln schon zerlegbar sind. Gewöhnliche Darstellungen kann man als $\mathbb {C}$ G-Moduln betrachten.

Um Klassen endlicher Untergruppen der GL(V) zu klassifizieren, reicht es deswegen, die irreduziblen Gruppen zu klassifizieren. Alle weiteren erhält man dann als direkte Produkte.

Die irreduziblen endlichen komplexen Spiegelungsgruppen wurden 1954 von Shephard und Todd vollständig klassifiziert [G. C. Shephard, J. A. Todd, "Finite Unitary Reflection Groups", Canad. J. Math., 6, (1954), 274-304]: es gibt sechs Serien und 34 exceptionelle irreduzible komplexe Spiegelungsgruppen.

In Analogie zu den Coxetergraphen für reelle Spiegelungsgruppen wurden auch für komplexe Spiegelungsgruppen Präsentationen via Graphen "à la Coxeter" entwickelt, die allerdings wesentlich komplizierter als die Graphen reeller Spiegelungsgruppen sind. 1967 stellte Coxeter selbst für einige Gruppen Graphen vor [H. M. S. Coxeter, "Finite groups generated by unitary reflections", Hamburg Abh. 31, (1967), 125-135], vollständige Listen finden sich bei Cohen [A. M. Cohen, "Finite complex reflection groups", Ann. Scient. Ec. Norm. Sup 4 t 9, (1976), 379-436] oder bei Broué, Malle und Rouquier [M. Broué, G. Malle, R. Rouquier, "On complex reflection groups and their associated Braid groups", CMS Conference Proceedings, 16, (1995), 1-13], wobei sich die Graphen für einzelne Gruppen zum Teil deutlich unterscheiden.

G₃₄ =	$\langle$ s, t, u, v, w, x \| s² = t² = u² = v² = w² = x² = 1, sts = tst, su = us, sw = ws,
	sv = vs, sx = xs, tut = utu, twt = wtw, tv = vt, tx = xt, wuwtwu = twuwtw,
	uwu = wuw, uvu = vuv, ux = xu, vw = wv, vxv = xvx, xw = wx $\rangle$

Im Übersichtsartikel von Hughes [M. C. Hughes, "Complex Reflection Groups", Communications in Algebra,18 (12), (1990), 3999-4029] findet man drei verschiedene Graphen für G₃₄:

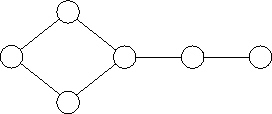
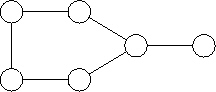
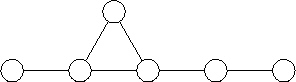
Für jede komplexe Spiegelungsgruppe existiert eine Familie von "Invarianten", deren Zahl nur von der Dimension abhängt.

Lemma 1.6 (vgl. [M. Broué, G. Malle, R. Rouquier, "On complex reflection groups and their associated Braid groups", CMS Conference Proceedings, 16, (1995), 1-13])

Zu jeder komplexen Spiegelungsgruppe G $\subseteq$ GL(V) existiert eine Familie von r : =Dimension von G natürlichen Zahlen d₁, d₂,..., d_r, so daß gilt:

| G| = d₁^.d₂^....^.d_r.
N^*(G) = $\sum_{i=1}^{r}$ (d_i - 1).
| Z(G)| = ggt(d₁, d₂,..., d_r),
Z(G) bezeichne das Zentrum von G.

d₁,..., d_r werden die "Grade" von G genannt.