Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Gruppentheorie - Nilpotente, auflösbare und polyzyklische Gruppen - Struktur nilpotenter Gruppen

Struktursatz fur endliche nilpotente Gruppen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Sei $ G$ eine endliche Gruppe. Dann sind die folgenden Aussagen äquivalent:
a)
$ G$ ist nilpotent.
b)
$ G$ ist das direkte Produkt ihrer Sylowgruppen.
c)
Jede Sylowgruppe von $ G$ ist normal in $ G$.
Insbesondere gilt:
(i)
Endliche $ p$ - Gruppen sind nilpotent.
(ii)
Ist $ G$ eine endliche $ p$ - Gruppe, dann ist $ Z(G) \neq 1$.
Der Beweis gliedert sich in folgende Teilschritte:
Schritt 1:
Beweis von (ii):

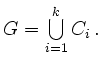Es seien $ C_1 , \ldots C_k$ die Konjugationsklassen von $ G$ und $ g_i$ sei ein Repräsentant von $ C_i$. Weiter sei $ g_1=e$. Man schreibe $ G$ nun als $ G=\bigcup \limits_{i=1}^k C_i\,.$ Es gilt dann

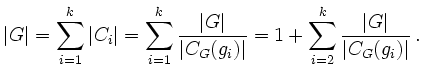
$\displaystyle \vert G\vert=\sum \limits_{i=1}^k\vert C_i\vert=\sum \limits_{i=1... ...g_i)\vert}=1+\sum \limits_{i=2}^k \frac{\vert G\vert}{\vert C_G(g_i)\vert} \,. $

Angenommen es ist $ Z(G)=1$, dann folgt $ C_G(g_i) \lneqq G$ für $ i \geq 2$. Nach dem Satz von Lagrange gilt dann $ \frac{\vert C_i\vert}{C_G(g_i)}=p^{a_i}$ mit $ a_i > 0$. Es folgt dann aber $ p^n=\vert G\vert=1+pm$ mit $ m>0$, und damit $ 1 \equiv 0 \mod p$. Der Widerspruch liefert also $ Z(G) \neq 1$.

Schritt 2:
Beweis von (i):

Abelsche Gruppen sind nilpotent. Die Erweiterungseigenschaft nilpotenter Gruppen (mit zentralem Normalteiler), Schritt 1 und Induktion liefern die Behauptung.

Schritt 3:
Behauptung: Endliche direkte Produkte nilpotenter Gruppen sind nilpotent.

Beweis: Für $ G=K \times H$ ist $ L_i(G) \times L_i(H)$, da $ [k,h]=1$ ist für $ k \in K$ und $ h \in H$. Damit ist $ G$ nilpotent, wenn $ K$ und $ H$ nilpotent sind.

Die Behauptung zeigt $ b) \Rightarrow a)$.

Schritt 4:
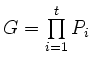Behauptung: Ist jede Sylowgruppe von $ G$ normal, dann ist $ G= \prod \limits_{i=1}^t P_i$ mit $ P_i=p_1-$Sylowgruppe. Ist umgekehrt $ G$ das Produkt von Sylowgruppen, dann ist jede Sylowgruppe normal.

Beweis: Die Richtung $ '\Rightarrow'$ zeigt man mit Induktion nach der Anzahl der Primteiler von $ \vert G\vert$. Die Richtung $ '\Leftarrow'$ ist trivial.

Diese Behauptung zeigt b) $ \Leftrightarrow c)$.

Schritt 5:
Behauptung: Eine endliche abelsche Gruppe ist direktes Produkt ihrer Sylowgruppen.

Beweis: Folgt direkt aus dem Hauptsatz über endlich erzeugt abelsche Gruppen.

Schritt 6:
Behauptung: Besitzt $ G/Z(G)$ normale Sylowgruppen, dann auch $ G$.

Beweis: Seien $ P_1,P_2 \in Syl_p(G)$ und $ \kappa:G \rightarrow G/Z(G)$ die kanonische Faktorabbildung. Dann ist $ \kappa(P_1),\kappa(P_2) \in Syl_p(G/Z(G))$. Nach Voraussetzung gilt also $ \kappa(P_1)=\kappa(P_2)$. Sei $ x\in P_1\setminus P_2$, dann existiert ein $ y \in P_2$ mit $ \kappa(x)=\kappa(y)$ und damit ein $ z\in Z(G)=ker(\kappa)$ mit $ x=zy$. Da $ z$ zentral ist, gibt es gilt dann $ x^m=z^my^m$. $ z$ hat also $ p-$Potenzordnung, denn $ x$ und $ y$ haben $ p-$Potenzordnung. Also ist $ z\in P_z$, wobei $ P_z$ die $ p-$Sylowgruppe von $ Z(G)$ ist ($ Z(G)$ ist abelsch. Es gibt also genau eine $ p-$Sylowgruppe). Es ist $ P_z \ char \ Z(G)$ und $ Z(G) \ char \ G$ und damit $ P_z \ char \ G$. Insbesondere ist $ P_z \unlhd G$. Nach dem Sylowsatz ist $ P_z \subset P \in Syl_p(G)$ und alle Sylowgruppen sind konjugiert. $ P_z$ ist also in jeder $ p-$Sylowgruppe von $ G$ enthalten. Insbesondere gilt $ P_z \subset P_2$, und damit $ zy=x \in P_2$, was aber nicht möglich ist. Also gilt $ P_1=P_2$ und $ p-$Sylowgruppen von $ G$ sind normal.

Beweisabschluss:
Ist $ G$ nilpotent, dann ist $ Z(G) \neq 1$. Sei $ L_{c+1}(G)=1$ und $ c$ die Nilpotenzklasse von $ G$, dann ist $ 1\neq L_c(G)$ und $ 1=L_{c+1}(G)=[G,L_c(G)]$. Also ist $ L_c(G)\leq Z(G)$. Mit den Schritten 5 und 6 folgt dann a) $ \Rightarrow$ b) Induktion.

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 14.11.2008