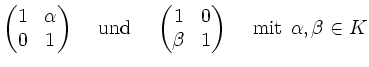Sei
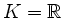 oder
oder
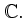
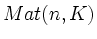 bezeichne die Menge der n
bezeichne die Menge der n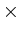 n-Matrizen mit Einträgen aus
n-Matrizen mit Einträgen aus 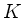 .
.
Die Einheitengruppe von 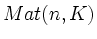 heisst allgemeine lineare Gruppe.
heisst allgemeine lineare Gruppe.
(Autor: Borgart)
Sei
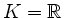 oder
oder
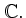 Die Menge
bildet zusammen mit der Matrixmultiplikation eine Gruppe und heisst spezielle lineare Gruppe.
Die Menge
bildet zusammen mit der Matrixmultiplikation eine Gruppe und heisst spezielle lineare Gruppe.
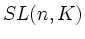 kann man als den Kern des Homomorphismus
charakterisieren.
Insbesondere gilt dann:
kann man als den Kern des Homomorphismus
charakterisieren.
Insbesondere gilt dann:
(Autor: Borgart)
Sei 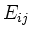 die n
die n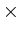 n-Matrix,
die im Schnittpunkt der i-ten Zeile und der j-ten Spalte eine 1, sonst überall 0 hat.
Als Elementarmatrizen werden bezeichnet:
n-Matrix,
die im Schnittpunkt der i-ten Zeile und der j-ten Spalte eine 1, sonst überall 0 hat.
Als Elementarmatrizen werden bezeichnet:
-
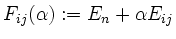 für
für
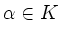 und
und
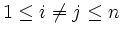
-
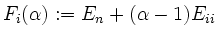 für
für
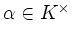 und
und
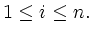
Es gilt also
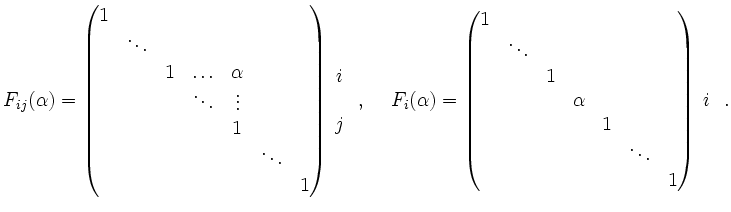
Durch leichtes Nachrechnen sieht man, dass
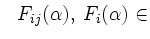 GL(n,K) und
GL(n,K) und
Multiplikation einer Matrix 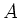 von links (rechts) mit
von links (rechts) mit
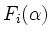 bedeutet Multiplikation
der i-ten Zeile (Spalte) mit
bedeutet Multiplikation
der i-ten Zeile (Spalte) mit 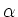 ,
,
Multiplikation der Matrix 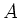 von links (rechts) mit
von links (rechts) mit
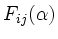 bedeutet Addition des
bedeutet Addition des 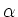 -fachen der j-ten Zeile (i-ten Spalte)
-fachen der j-ten Zeile (i-ten Spalte)
zur
i-ten Zeile (j-ten Spalte). Man spricht von ´´elementaren Zeilen- bzw. Spaltenumformungen``.
(Autor: Borgart)
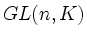 wird von den Elementarmatrizen erzeugt.
wird von den Elementarmatrizen erzeugt.
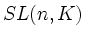 wird von den Elementarmatrizen vom Typ(1) erzeugt (d. h. Matrizen der Form
wird von den Elementarmatrizen vom Typ(1) erzeugt (d. h. Matrizen der Form
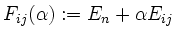 für
für
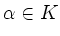 und
und
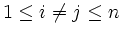 ).
).
Insbesondere wird die Gruppe 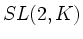 von den Matrizen
erzeugt.
von den Matrizen
erzeugt.
(Autor: Borgart)
Jede Matrix 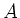 aus
aus 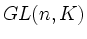 kann durch elementare Zeilenumformungen in die Einheitsmatrix
übergeführt werden, d.h.
kann durch elementare Zeilenumformungen in die Einheitsmatrix
übergeführt werden, d.h. 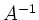 , also auch
, also auch 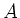 , ist Produkt von Elementarmatrizen.
Umgekehrt liegen alle Elementarmatrizen in
, ist Produkt von Elementarmatrizen.
Umgekehrt liegen alle Elementarmatrizen in 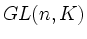 .
.
(Autor: Borgart)
Offensichtlich sind die Matrizen vom Typ(1) in 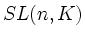 enthalten.
enthalten.
Sei
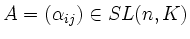 beliebig. Wir zeigen, dass
beliebig. Wir zeigen, dass 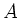 ein endliches Produkt
aus den Matrizen vom Typ (1) ist:
ein endliches Produkt
aus den Matrizen vom Typ (1) ist:
Falls
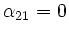 , dann muss es ein i
, dann muss es ein i 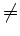 2 geben, so dass
2 geben, so dass
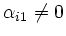 ,
da
,
da 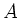 sonst nicht invertierbar sein kann. Addition der i-ten Zeile zur zweiten ergibt eine
neue Matrix (
sonst nicht invertierbar sein kann. Addition der i-ten Zeile zur zweiten ergibt eine
neue Matrix (
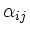 ) mit
) mit
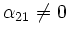 . Dies entspricht der Multiplikation der
Matrix
. Dies entspricht der Multiplikation der
Matrix 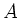 von links mit der Matrix
von links mit der Matrix 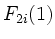 . Also können wir im weiteren annehmen, dass
. Also können wir im weiteren annehmen, dass
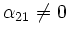 .
.
Addition des
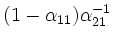 -fachen der zweiten Zeile zur ersten ergibt eine
Matrix
-fachen der zweiten Zeile zur ersten ergibt eine
Matrix
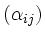 mit
mit
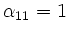 . Durch Addition des
. Durch Addition des
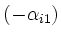 -fachen der
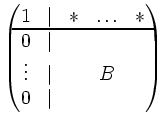
ersten Zeile zur i-ten, i > 1, erhalten wir schließlich eine Matrix der Form
mit
-fachen der
ersten Zeile zur i-ten, i > 1, erhalten wir schließlich eine Matrix der Form
mit
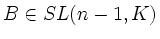 . Fahren wir so fort,
so ergibt sich nach endlich vielen Multiplikationen von
. Fahren wir so fort,
so ergibt sich nach endlich vielen Multiplikationen von  mit den Elementarmatrizen von Typ (1)
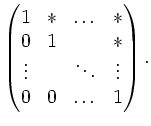
eine obere Dreicksmatrix, deren Hauptdiagonalelemente gleich 1 sind:
Hieraus entsteht aber in ähnlicher Weise durch elementare Zeilenumformungen vom Typ (1) die
Einheitsmatrix. Da das Inverse einer Matrix vom Typ (1) ebenso eine Matrix vom Typ (1) ist,
ist
mit den Elementarmatrizen von Typ (1)
eine obere Dreicksmatrix, deren Hauptdiagonalelemente gleich 1 sind:
Hieraus entsteht aber in ähnlicher Weise durch elementare Zeilenumformungen vom Typ (1) die
Einheitsmatrix. Da das Inverse einer Matrix vom Typ (1) ebenso eine Matrix vom Typ (1) ist,
ist  ein Produkt aus endlich vielen Matrizen vom Typ (1).
ein Produkt aus endlich vielen Matrizen vom Typ (1).
(Autor: Borgart)
| |
automatisch erstellt
am 14.11.2008 |


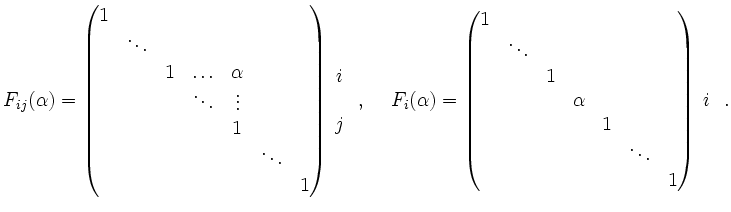
![]() GL(n,K) und
GL(n,K) und
![]() von links (rechts) mit
von links (rechts) mit
![]() bedeutet Multiplikation
der i-ten Zeile (Spalte) mit
bedeutet Multiplikation
der i-ten Zeile (Spalte) mit ![]() ,
,
![]() von links (rechts) mit
von links (rechts) mit
![]() bedeutet Addition des
bedeutet Addition des ![]() -fachen der j-ten Zeile (i-ten Spalte)
-fachen der j-ten Zeile (i-ten Spalte)