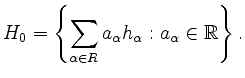Für
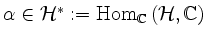 setze
setze
Eine Linearform
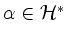 heißt Wurzel von
heißt Wurzel von 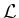 bzgl.
bzgl. 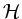 , falls
, falls
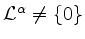 und
und
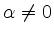 ist.
ist.
Die Menge der Wurzeln, genannt Wurzelsystem, wird mit
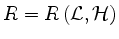 bezeichnet.
bezeichnet.
Es gelten folgende Aussagen:
-
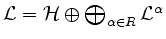
-
![$ \left[{\cal L}^\alpha,{\cal L}^\beta\right]\subseteq{\cal L}^{\alpha+\beta}$](/inhalt/aussage/aussage1381/img10.png) für
für 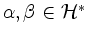
-
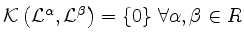 mit
mit 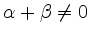
- Die Restriktion von
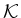 auf
auf
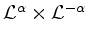 ist für jedes
ist für jedes
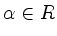 nicht-ausgeartet, ebenso die Restriktion auf
nicht-ausgeartet, ebenso die Restriktion auf 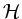 .
.
- Für alle
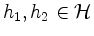 gilt
gilt
- Für alle
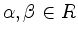 und alle
und alle
![$ h\in\left[{\cal L}^\alpha,{\cal L}^{-\alpha}\right]$](/inhalt/aussage/aussage1381/img20.png) gibt es ein
gibt es ein
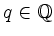 so, dass
so, dass
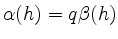 ist.
ist.
- Zu jedem
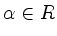 und zu jedem
und zu jedem
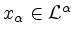 gibt es
gibt es
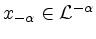 und
und
![$ h_\alpha\in\left[{\cal L}^\alpha,{\cal L}^{-\alpha}\right]$](/inhalt/aussage/aussage1381/img25.png) so, dass
so, dass
![$ \left[h_\alpha,x_\alpha\right]=2x_\alpha,~\left[h_\alpha,x_{-\alpha}\right]=-2x_{-\alpha},~\left[x_\alpha,x_{-\alpha}\right]=h_{\alpha}$](/inhalt/aussage/aussage1381/img26.png) gilt.
gilt.
-
![$ \operatorname{dim}({\cal L}^\alpha)=\operatorname{dim}\left[{\cal L}^\alpha,{\cal L}^{-\alpha}\right]=1~\forall\alpha\in R$](/inhalt/aussage/aussage1381/img27.png) .
.
Desweiteren gilt:
Ist 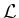 eine komplexe, halbeinfache Lie-Algebra,
eine komplexe, halbeinfache Lie-Algebra, 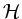 eine Cartansche Teilalgebra von
eine Cartansche Teilalgebra von 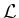 ,
, 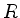 das zugehörige Wurzelsystem und
das zugehörige Wurzelsystem und
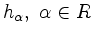 , wie oben, dann gilt:
, wie oben, dann gilt:
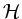 wird aufgespannt von
wird aufgespannt von
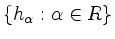
-
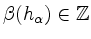 für alle
für alle
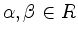
-
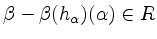 für alle
für alle
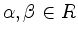
- Für alle
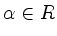 und
und
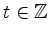 gilt
gilt
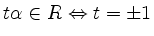
Es bezeichne 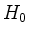 der von
der von
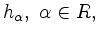 aufgespannte
aufgespannte
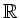 -Vektorraum, also
-Vektorraum, also
Nach Obigem gilt
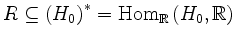 ,
,
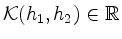 und
und
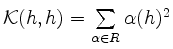 für alle
für alle
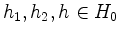 . Also ist die Restriktion der Killing-Form auf
. Also ist die Restriktion der Killing-Form auf 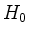 positiv definit.
positiv definit.
Mit Hilfe des
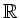 -Vektorraum-Isomorphismus
-Vektorraum-Isomorphismus
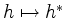 ,
,
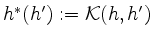 von
von 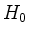 auf
auf 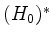 erhalten wir eine positiv-definite, symmetrische Bilinearform auf
erhalten wir eine positiv-definite, symmetrische Bilinearform auf 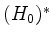 , definiert durch
, definiert durch
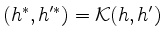
für
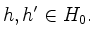
Damit wird das Wurzelsystem
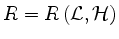 zu einer Teilmenge eines euklidischen Vektorraumes.
zu einer Teilmenge eines euklidischen Vektorraumes.
Für alle
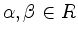 ,
, 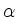 nicht proportional zu
nicht proportional zu 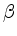 , gibt es
, gibt es
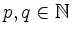 so, dass gilt:
so, dass gilt:
-
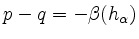
-
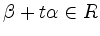 für
für
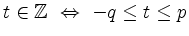
(Autor: Hablizel)
Sei 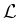 eine komplexe, halbeinfache Lie-Algebra,
eine komplexe, halbeinfache Lie-Algebra, 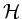 eine Cartansche Teilalgebra von
eine Cartansche Teilalgebra von 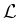 und
und 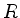 das zugehörige Wurzelsystem. Eine Teilmenge
das zugehörige Wurzelsystem. Eine Teilmenge 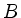 von
von 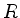 heißt Basis von
heißt Basis von 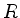 , wenn gilt
, wenn gilt
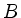 ist linear unabhängig über
ist linear unabhängig über
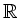
- jede Wurzel
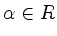 hat eine Darstellung
hat eine Darstellung
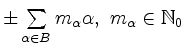
Gilt für 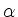 das Pluszeichen (Minuszeichen), dann heißt
das Pluszeichen (Minuszeichen), dann heißt 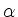 positive (negative) Wurzel bzgl. B. Die Menge der positiven (negativen) Wurzeln wird mit
positive (negative) Wurzel bzgl. B. Die Menge der positiven (negativen) Wurzeln wird mit 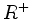 (
(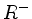 ) bezeichnet (es gilt
) bezeichnet (es gilt 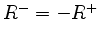 ).
).
Es gelten folgende Aussagen:
Jedes Wurzelsystem hat eine Basis. Ist 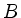 eine Basis, so gilt (außer
eine Basis, so gilt (außer
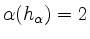 für
für
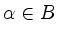 ):
):
-
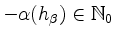 für
für
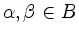 ,
,
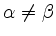
-
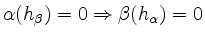 für
für
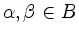
Man verifiziert leicht, dass 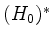 von
von 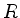 aufgespannt wird, nach obigem also auch von jeder Basis von
aufgespannt wird, nach obigem also auch von jeder Basis von 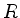 . Benutzt man noch, dass
. Benutzt man noch, dass 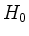 eine reelle Form von
eine reelle Form von 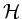 ist, so folgt:
ist, so folgt:
Ist 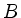 eine Basis von
eine Basis von
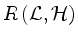 , so ist
, so ist 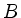 eine
eine
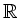 -Basis von
-Basis von 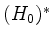 und eine
und eine
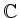 -Basis von
-Basis von
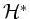 . Die
. Die
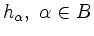 bilden eine
bilden eine
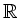 -Basis von
-Basis von 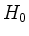 und eine
und eine
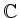 -Basis von
-Basis von 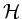 .
.
(Autor: Hablizel)
| |
automatisch erstellt
am 14.11.2008 |


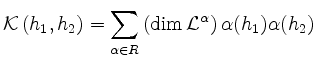
![]() eine komplexe, halbeinfache Lie-Algebra,
eine komplexe, halbeinfache Lie-Algebra, ![]() eine Cartansche Teilalgebra von
eine Cartansche Teilalgebra von ![]() ,
, ![]() das zugehörige Wurzelsystem und
das zugehörige Wurzelsystem und
![]() , wie oben, dann gilt:
, wie oben, dann gilt: