Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Mathematik 1 für Informatik und Softwaretechnik - Übungsblätter - Aufgabenblatt 14

Blatt 14 Aufgabe 3

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Überprüfen Sie die folgenden Reihen auf Konvergenz bzw. Divergenz. Untersuchen Sie die Reihen e), f) und g) auf absolute Konvergenz und geben Sie bei den Reihen h) und i) an, für welche größte Teilmenge von $ \mathbb{C}$ die Reihe jeweils konvergiert.

\begin{displaymath} \left. \begin{array}{rl@{\qquad\ }rl@{\qquad\ }rl} {\bf a)}&... ...\sum\limits_{n=1}^\infty\, \frac{z^n}{n}\,. \end{array}\right. \end{displaymath}

Lösung:
zu a) keine Angabe , konvergent , nicht konvergent
zu b) keine Angabe , konvergent , nicht konvergent
zu c) keine Angabe , konvergent , nicht konvergent
zu d) keine Angabe , konvergent , nicht konvergent
zu e) keine Angabe , absolut konvergent, konvergent aber nicht absolut konvergent, nicht konvergent
zu f) keine Angabe , absolut konvergent, konvergent aber nicht absolut konvergent, nicht konvergent
zu g) keine Angabe , absolut konvergent, konvergent aber nicht absolut konvergent, nicht konvergent
zu h) konvergiert für
  keine Angabe ,
  kein 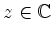$ z \in \mathbb{C}$ , also divergent
  $ z =0$ ,
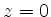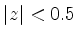  $ \vert z\vert <0.5$ ,
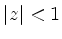  $ \vert z\vert <1$ ,
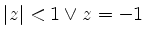  $ \vert z\vert <1 \vee z=-1$ ,
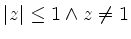  $ \vert z\vert \leq 1 \wedge z \ne 1$ ,
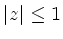  $ \vert z\vert \leq 1$ ,
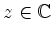  alle $ z \in \mathbb{C}$ .
zu i) konvergiert für
  keine Angabe ,
  kein 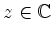$ z \in \mathbb{C}$ , also divergent
  $ z =0$ ,
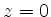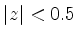  $ \vert z\vert <0.5$ ,
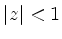  $ \vert z\vert <1$ ,
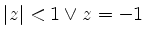  $ \vert z\vert <1 \vee z=-1$ ,
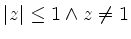  $ \vert z\vert \leq 1 \wedge z \ne 1$ ,
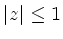  $ \vert z\vert \leq 1$ ,
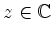  alle $ z \in \mathbb{C}$ .


   

(Aus: Mathematik 1 für Informatik und Softwaretechnik WS05/06; Teufel/Röhrl)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 17.2.2006