Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: MATLAB - Anwendungen

Lösung gewöhnlicher Differentialgleichungen mit MATLAB

[vorangehende Seite]   [Gesamtverzeichnis][Seitenübersicht]

Zur Lösung von Anfangswertproblemen für gewöhnliche Differentialgleichungen in Standardform,

$\displaystyle u^\prime(t) = f(t,u(t)),\quad u(t_0) = u_0 \,, $

stehen in Matlab eine Reihe von Programmen zur Verfügung. Eine generell anwendbare Routine ist die Matlab-Funktion

[t_steps, u] = ode45(f, t_range, u_0),

die auf dem eingebetteten Runge-Kutta-Verfahren von Dormand-Prince basiert.

Die rechte Seite der Differentialgleichung wird als function-handle übergeben. Für einen Skalar $ t$ und einen Spaltenvektor $ u$ berechnet die entsprechende Matlab-Funktion $ f$ den Spaltenvektor $ f(t,u)$. Mit t_range = [t_0; t_end] wird das Zeitintervall spezifiziert. Schließlich ist der Spaltenvektor u_0 der Anfangswert $ u(t_0)$. Das Programm ode45 gibt die Lösung an den zur Berechnung benutzten Zwischenzeiten t_steps(k) als Zeilenvektoren u(k,:) zurück.

Als Beispiel wird die durch

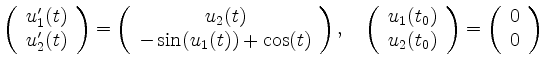
$\displaystyle \left(\begin{array}{c} u_1^\prime(t) \\ u_2^\prime(t) \end{array}... ...u_2(t_0) \end{array}\right) = \left(\begin{array}{c} 0 \\ 0 \end{array}\right) $

beschriebene erzwungene Schwingung eines Pendels berechnet: 

f=@(t,u) ([u(2); -sin(u(1))+cos(t)/3]);
t_range = [0; 40]; u_0 = [0; 0];
[t_steps, u] = ode45(f, t_range, u_0);

Die Lösung kann auf verschiedene Weise visualisiert werden. Mit 

plot(t_steps, u);

werden die beiden Lösungskomponenten als Funktion von $ t$ gezeigt. Alternativ kann mit 

plot(u(:,1),u(:,2));

die Trajektorie in der Phasenebene dargestellt werden.

\includegraphics[width=.8\linewidth]{aussage713_trajektorie}

Möchte man die Lösung zu bestimmten vorgegebenen Zeiten $ t$ berechnen, so können diese in dem Vektor t_range spezifiziert werden, z.B. t_range = [0: 0.1: 40] Die Routine ode45 erlaubt auch eine Reihe weiterer Optionen, wie beispielsweise Toleranzen oder Vorzeichenrestriktionen.

[vorangehende Seite]   [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.2.2008