
Mathematik-Online-Kurs: LaTeX - Darstellung mathematischer Ausdrücke

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Kurs: LaTeX - Darstellung mathematischer Ausdrücke | |
Funktionen, Operationen und Relationen |
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
\arccos \cos \csc \exp \ker \limsup \min \sinh
\arcsin \cosh \deg \gcd \lg \ln \Pr \sup
\arctan \cot \det \hom \lim \log \sec \tan
\arg \coth \dim \inf \liminf \max \sin \tanh
Eigene Funktionen können mit Hilfe des Befehls
aus dem amsmath-Paket dargestellt werden.\operatorname{Funktionsname}
Als Operationen stehen unter anderem die folgenden Symbole zur Verfügung:

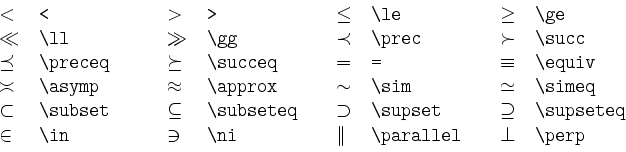
\not
negiert werden. Zum Beispiel ist
\not\in
\not=
\not\subset
\not\equiv
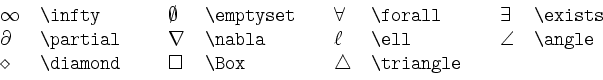
\documentclass[12pt]{article}
\usepackage[ngerman]{babel}
\usepackage[latin1]{inputenc}
\usepackage{amssymb,amsmath}
\thispagestyle{empty}
\setlength{\parindent}{0cm}
\begin{document}
Die Folge $(a_n)=a_1,a_2,\dots$, $n\in\mathbb{N}$, besitzt den
Grenzwert $a$, d.h.
\[
\lim_{n\to\infty} a_n=a\,,
\]
genau dann, wenn
\[
\forall \, \varepsilon>0 \; \exists \, n_\varepsilon: \forall
n>n_\varepsilon \text{ gilt } |a-a_n|<\varepsilon \, .
\]
Die Divergenz des Vektorfelds $\vec{F}(x,y,z)$ ist gegeben durch
\[
\operatorname{div} \vec{F}=\partial_x\vec{F}+\partial_y\vec{F}
+\partial_z\vec{F}\,.
\]
Man beachte, dass hier \verb|\operatorname{div}| zur Darstellung
der Divergenz verwendet wurde, da der Befehl \verb|\div| das Symbol
$\div$ ergibt. Die Darstellung $div \vec{F}$ wäre ebenso falsch, da
$div$ hier das Produkt der Variablen $d$, $i$ und $v$ ist. Zudem
werden bei Verwendung von $\operatorname{div} \vec{F}$ im Gegensatz
zu ${\rm div} \vec{F}$ die Abstände korrekt gesetzt.
\end{document}
ergibt
![\includegraphics[width=14cm]{bsp_math_funktionen_symbole.eps}](/inhalt/beispiel/beispiel1083/img1.png)
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 24.2.2009 |