Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: LaTeX - Darstellung mathematischer Ausdrücke

Produkte, Summen und Integrale

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die mit \prod, \sum und \int erzeugten Symbole $ \prod$ , $ \sum$ und $ \int$ für Produkt, Summe und Integral haben eine besondere Funktionalität. Ihre Darstellungsgrößen und Verhaltensweisen bei Angabe von unteren und oberen Grenzen unterscheiden sich je nach mathematischer Umgebung. So ergibt 
  \prod_{k=1}^n k = n! \,,\quad \sum_{k=1}^n k=\frac{n(n+1)}{2}\,,
  \quad \int_0^{2\pi}\sin t\,dt=0
in mathematischen Fließtextumgebungen wie $ $ die Ausgabe
$ \prod_{k=1}^n k = n! \,,\quad \sum_{k=1}^n k=\frac{n(n+1)}{2}\,, \quad \int_0^{2\pi}\sin t\,dt=0 $\,,
um keine zu großen Unter- und Überlängen zu produzieren. Dagegen wird bei abgesetzten mathematischen Umgebungen wie \[ \] die Ausgabe

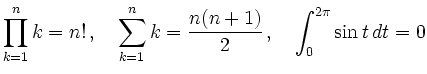
$\displaystyle \prod_{k=1}^n k = n! \,,\quad \sum_{k=1}^n k=\frac{n(n+1)}{2}\,, \quad \int_0^{2\pi}\sin t\,dt=0 $

erzeugt. Unabhängig von der Art der mathematischen Umgebung kann mit Hilfe der beiden Befehle \limits bzw. \nolimits direkt im Anschluss an \prod, \sum und \int erzwungen werden, dass die Grenzen über bzw. hinter dem Symbol erscheinen.

Mehrfachintegrale können mit Hilfe der Befehle \iint, \iiint und \iiiint aus dem amsmath-Paket erzeugt werden. Ein Beispiel hierfür ist der Satz von Gauß

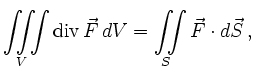
$\displaystyle \iiint\limits_V \operatorname{div} \vec{F} \, dV = \iint\limits_S \vec{F}\cdot d\vec{S}\,, $

mit dem Quelltext 
  \[
    \iiint\limits_V \operatorname{div} \vec{F} \, dV 
    = \iint\limits_S \vec{F}\cdot d\vec{S}
  \]
Man beachte dabei, dass bei Mehrfachintegralen die Integrationsbereiche unter den Integralzeichen zentriert angegeben werden, was durch die jeweilige Angabe von \limits erzielt wurde.

Eine automatische Größenanpassung und Positionierung von Grenzen erfolgt auch bei den folgenden Symbolen:

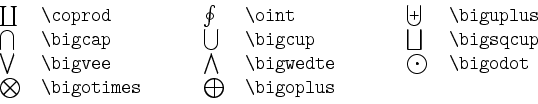
\begin{tabular}{lp{3cm}lp{3cm}lp{3cm}lp{3cm}} $\coprod$\ & \verb\vert\coprod\ve... ...b\vert\bigotimes\vert & $\bigoplus$\ & \verb\vert\bigoplus\vert \end{tabular}

(Autor: Joachim Wipper)
Der Quelltext 
  Die Lagrange-Form des Interpolationspolynoms der $n+1$ Datenpunkte 
  $(x_i, f_i)$ ist gegeben durch
  \[
    p(x)=\sum_{i=0}^n f_{i}q_{i}(x) \quad\mbox{mit}\quad
    q_{i}(x)=\prod_{\substack{k=0 \\ k\neq i}}^n
    \frac{x-x_{k}}{x_{i}-x_{k}}\,.
  \]
ergibt
\includegraphics[width=14cm]{bsp_summen_produkte.eps}
Die mehrzeilige Angabe unter dem Produktzeichen wurde dabei mit Hilfe des Befehls
\substack{ Zeile 1 \\ Zeile 2 \\ ...}
aus dem Paket amsmath realisiert.

(Autor: Joachim Wipper)
Der Quelltext 
  Kurvenintegral (normale Anordnung der Grenzen):
  \[
    \int_C U = \int_a^b U \big(\vec{r}\,(t)\big)\,|\vec{r}\,'(t)|\,dt
  \]
  Arbeitsintegral (Verwendung von \verb|\limits|):
  \[
    \int\limits_C \vec{F} \cdot d\vec{r} 
      =\int\limits_a^b \vec{F} \big(\vec{r}\,(t)\big)
      \cdot \vec{r}\,'(t)\,dt
  \]
  Fluss durch eine Sphäre mit Radius $a$ (Mehrfachintegral jeweils mit Grenzen):
  \[
    \int_0^\pi \int_0^{2\pi} F_r a^2 \sin\vartheta \, d\varphi d\vartheta
  \]
  Satz von Green (Mehrfachintegrale über Bereiche mit \verb|\limits|):
  \[
    \iint\limits_S (U \operatorname{grad} W)\cdot d\vec{S} 
    =\iiint\limits_V (\operatorname{grad} U\cdot 
     \operatorname{grad} W +U\Delta W)\,dV
  \]
ergibt
\includegraphics[width=14cm]{bsp_integrale.eps}

(Autor: Joachim Wipper)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 24.2.2009